Regression
Introduction
Regression analysis is a conceptually simple method for investigating functional relationships between variables. The relationship is expressed in the form of an equation or a model connecting the response or dependent variable and one or more explanatory or predictor variables.
We denote the response variable by
The general regression model is specified as:
An example is the linear regression model:
where
Steps in Regression Analysis
1. Statement of the problem
Formulation of the problem includes determining the questions to be addressed.
2. Selection of Potentially Relevant Variables
We select a set of variables that are thought by the experts in the area of study to explain or predict the response variable.
Each of these variables could be qualitative or quantitative. A technique used in casse where the response variable is binary is called logistic regression. If all predictor variables are qualitative, the techniques used in the analysis of the data are called the analysis of variance techniques. If some of the predictor variables are quantitative while others are qualitative, regression analysis in these cases is called the analysis of covariance.
| Type | Conditions |
|---|---|
| Univariate | Only 1 quantitative RV |
| Multivariate | 2 or more quantitative RV |
| Simple | Only 1 predictor variable |
| Multiple | 2 or more predictor variables |
| Linear | All parameters enter the equation linearly, possibly after transformation of the data |
| Non-linear | The relationship between the response and some of the predictors is non-linear (no transformation to make parameters appear linearly) |
| Analysis of variance | All predictors are qualitative variables |
| Analysis of covariance | Some predictors are quantitative variables, others are qualitative |
| Logistic | The RV is qualitative |
3. Model specification
The form of the model that is thought to relate the response variable to the set of predictor variables can be specified initially by experts in the area of study based on their knowledge or their objective and/or subjective judgments.
We need to select the form of the function
4. Method of Fitting
We want to perform parameter estimation or model fitting after defining the model and collecting the data. the most commonly used method of estimation is called the least squares method. Other estimation methods we consider are the maximum likelihood method, ridge regression and the principal components method.
5. Model Fitting
The estimates of the regression parameters
6. Model Criticism and Selection
The validity of statistical methods depend on certain assumptions, about the data and the model. We need to address the following questions:
- What are the required assumptions?
- For each of these assumptions, how do we determine if they are valid?
- What can be done in cases where assumptions do not hold?
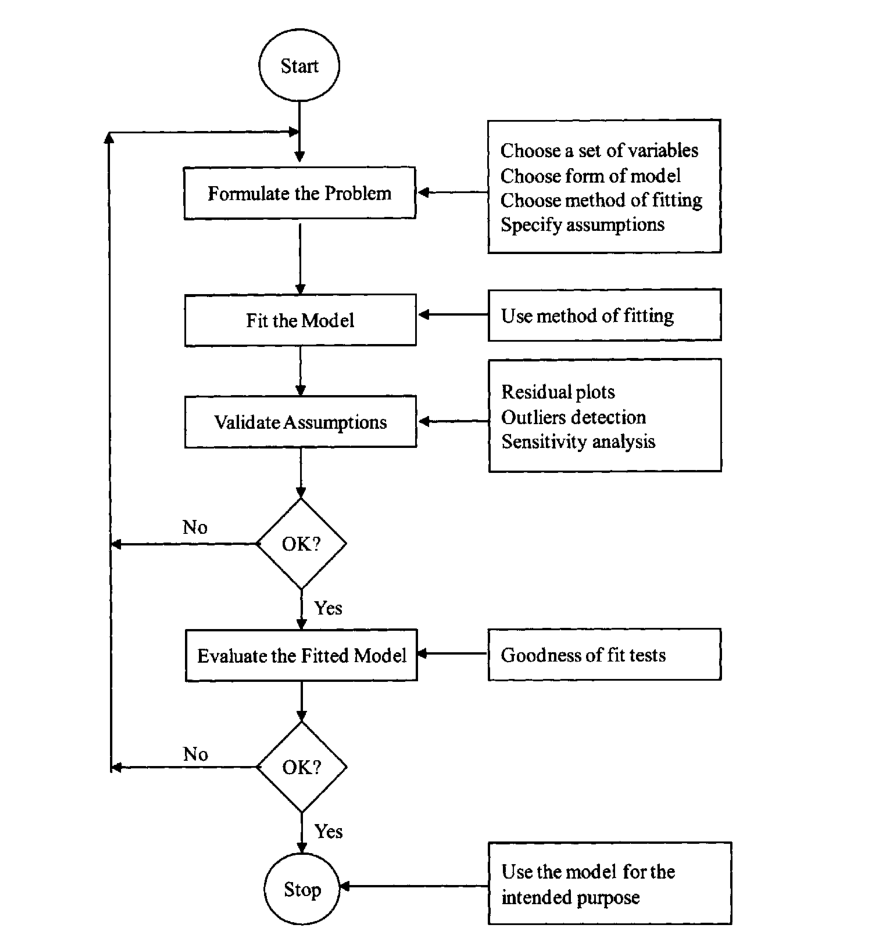
Figure 1: Flowchart illustrating the dynamic iterative regression process
Simple Linear Regression
Simple linear regression is a straightforward approach for predicting
a quantitative response
We describe this as regressing
We wish to measure both the direction and strength of the relationship
between
We use our training data to produce estimates
Let
The least squares approach chooses
If
where
We need to assess the accuracy of our estimates. How far off will a
single estimation of
where
Standard errors can be used to compute confidence intervals. A 95%
confidence interval is defined as a range of values such that with 95%
probability, the range will contain the true unknown value of the
parameter. For linear regression, the 95% confidence interval for
Standard errors can also be used to perform hypothesis tests on the coefficients. The most common hypothesis test involves testing the null hypothesis of:
versus the alternative hypothesis:
To test the null hypothesis, we need to determine whether
which measures the number of standard deviations that
It is a simple matter to compute the probability of observing any
number equal to
Assessing the accuracy of the model
Once we have rejected the null hypothesis in favour of the alternative hypothesis, it is natural to want to quantify the extent to which the model fits the data.
Residual Standard Error (RSE)
After we compute the least square estimates of the parameters of a linear model, we can compute the following quantities:
A fundamental equality in both simple and multiple regressions is
given by
The RSE provides an absolute measure of lack of fit of the model to
the data. But since it is measured in the units of
where
Note that the correlation coefficient
Multiple Linear Regression
We can extend the simple linear regression model to accommodate multiple predictors:
We choose
Unlike the simple regression estimates, the multiple regression coefficient estimates have complicated forms that are most easily represented using matrix algebra.
Interpreting Regression Coefficients
First, it may be interpreted as the change in
Centering and Scaling
The magnitudes of the regression coefficients in a regression equation depend on the unit of measurements of the variables. To make the regression coefficients unit-less, one may first center or scale the variables before performing regression computations.
When dealing with constant term models, it is convenient to center and scale the variables, but when dealing with no-intercept models, we need only to scale the variables.
A centered variable is obtained by subtracting from each observation
the mean of all observations. For example, the centered response
variable is
The centered variables can also be scaled. Two types of scaling are usually performed: unit-length scaling and standardizing.
Unit-length scaling of response variable
where:
The quantities
Unit length scaling has the following property:
The second type of scaling is called standardizing, which is defined by:
where
Since correlations are unaffected by centering or scaling, it is sufficient and convenient to deal with either unit-length scaled or standardized models.
Properties of Least-square Estimators
Under certain regression assumptions, the least-square estimators have the following properties:
-
The estimator
-
The estimator
-
-
The vector
Important Questions in Multiple Regression Models
We can answer some important questions using the multiple regression model:
1. Is there a relationship between the response and the predictors?
The strength of the linear relationship between
A quantity related to
If we do a hypothesis test on
which has a Stundent’s t-distribution with
If we are comparing
If the linear model is correct, one can show that:
and that provided
Hence, when there is no relationship between the response and the
predictors, one would expect the F-statistic to be close to 1. if
2. Deciding on important variables
It is possible that all of the predictors are associated with the
response, but it is more often the case that the response is only
related to a subset of the predictors. The task of determining which
predictors are associated is referred to as variable selection.
Various statistics can be used to judge the quality of a model. These
include Mallow’s
There are
- Forward selection: We begin with the null model – a model that contains an intercept but no predictors. We then fit p simple linear regressions and add to the null model the variable that results in the lowest RSS. We then add to that model the variable that results in the lowest RSS for the new two-variable model, and repeat.
- Backward selection: We start with all variables in the model, andd remove the variable with the largest p-value – that is the variable that is the least statistically significant. The new (p-1)-variable model is fit, and the variable with the largest p-value is removed, and repeat.
- Mixed selection. This is a combination of forward and backward-selection. We once again start with the null model. The p-values of the variables can become larger as new variables are added to the model. Once the p-value of one of the variables in the model rises above a certain threshold, they are removed.
3. Model Fit
Two of the most common numerical measures of model fit are the RSE
and
It turns out that
4. Predictions
Once we have fit the multiple regression model, it is straightforward
to predict the response
- The coefficient estimates
That is, the least squares plane:
is only an estimate for the true population regression plane:
This inaccuracy is related to the reducible error. We can compute a
confidence interval in order to determine how close
-
In practice, assuming a linear model for
-
Even if we knew
Qualitative Variables
Thus far our discussion had been limited to quantitative variables. How can we incorporate qualitative variables such as gender into our regression model?
For variables that take on only two values, we can create a dummy variable of the form (for example in gender):
and use this variable as a predictor in the equation. We can also use the {-1, 1} encoding. For qualitative variables that take on more than 2 values, a single dummy variable cannot represent all values. We can add additional variables, essentially performing a one-hot encoding.
Extending the Linear Model
The standard linear regression model provides interpretable results and works quite well on many real-world problems. However, it makes highly restrictive assumptions that are often violated in practice.
The two most important assumptions of the linear regression model are that the relationship between the response and the predictors are:
- additive: the effect of changes in a predictor
- linear: the change in the response
How can we remove the additive assumption? We can add an interaction
term for two variables
We can analyze the importance of the interaction term by looking at its p-value. The hierarchical principle states that if we include an interaction in a model, we should also include the main effects, even if the p-values associated with their coefficients are not significant.
How can we remove the assumption of linearity? A simple way is to use polynomial regression.
Potential Problems
When we fit a linear regression model to a particular data set, many problems may occur. Most common among these are the following:
- Non-linearity of the response-predictor relationships
- Correlation of error terms
- Non-constant variance of error terms
- Outliers
- High-leverage points
- Collinearity
Non-linearity of the Data
The assumption of a linear relationship between response and
predictors aren’t always true. Residual plots are a useful graphical
tool for identifying non-linearity. This is obtained by plotting the
residuals
If the residual plots show that there are non-linear associations in
the data, then a simple approach is to use non-linear transformations
of the predictors, such as
Correlation of Error Terms
An important assumption of the linear regression model is that the
error terms,
Non-constant Variance of Error Terms
Variances of the error terms may increase with the value of the response. One can identify non-constant variances in the errors, or heteroscedasticity, from the presence of a funnel shape in the residual plot.
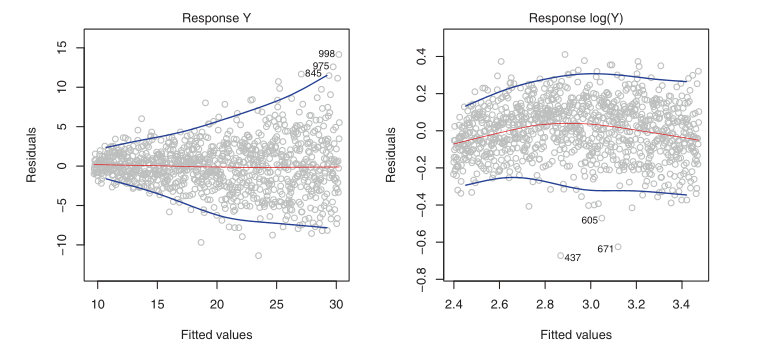
Figure 2: Left: the funnel shape indicates heteroscedasticity, Right: the response has been log transformed, and there is now no evidence of heteroscedasticity
Outliers
An outlier is a point from which
Residual plots can clearly identify outliers. One solution is to simply remove the observation, but care must be taken to first identify whether the outlier is indicative of a deficiency with the model, such as a missing predictor.
High Leverage Points
Observations with high leverage have an unusual value for
Collinearity
Collinearity refers to the situation in which two or more predictor variables are closely related to one another. The presence of collinearity can pose problems in the regression context: it can be difficult to separate out the individual effects of collinear variables on the response. A contour plot of the RSS associated with different possible coefficient estimates can show collinearity.
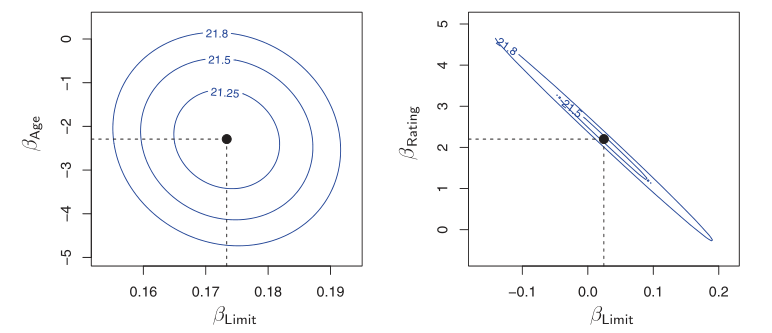
Figure 3: Left: the minimum value is well defined, Right: because of collinearity, there are many pairs
Another way to detect collinearity is to look at the correlation matrix of the predictors. An element of this matrix that is large in absolute value indicates a pair of highly correlated variables, and therefore a collinearity problem in the data.
Not all collinearity problems can be detected by inspection of the
correlation matrix: it is possible for collinearity to exist between
three or more variables even if no pairs of variables has a
particularly high correlation. This situation is called
multicollinearity. We instead compute the variance inflation factor
(VIF). The VIF is the ratio of the variance of
where
The data consists of
Linear Basis Function Models
We can extend the class of models by considering linear combinations of fixed non-linear functions of the input variables, of the form:
There are many choices on non-linear basis functions, such as the Gaussian basis function:
or the sigmoidal basis function:
Regression Diagnostics
In fitting a model to a given body of data, we would like to ensure that the fit is not overly determined by one or a few observations. The distribution theory, confidence intervals, and tests of hypotheses are valid and have meaning only if the standard regression assumptions are satisfied.
The Standard Regression Assumptions
Assumptions about the form of the model: The model that relates the
response
which implies that the ith observation can be written as:
Checking the linearity assumption can be done by examining the scatter
plot of
Assumptions about the errors: The errors
-
The error
-
The errors
-
The errors
-
The errors
Assumption about the predictors: Three assumptions are made here:
-
The predictor variables
-
The values
-
The predictor variables
Assumption about the observations: All observations are equally reliable and have an approximately equal role in determining the regression results.
A feature of the method of least squares is that minor violations of the underlying assumptions do not invalidate the inferences or conclusions drawn from the analysis in a major way. However, gross violations can severely distort conclusions.
Types of Residuals
A simple method for detecting model deficiencies in regression analysis is the examination of residual plots. Residual plots will point to serious violations in one or more of the standard assumptions when they exist. The analysis of residuals may lead to suggestions of structure or point to information in the data that might be missed or overlooked if the analysis is based only on summary statistics.
When fitting the linear model to a set of data by least squares, we obtain the fitted values:
and the corresponding ordinary least squares residuals:
The fitted values can also be written in an alternative form as:
where the
In multiple regression the
The value
When the standard assumptions hold, the ordinary residuals,
To over come the problem of unequal variances, we standardize the ith
residual
This is called the ith standardized residual because it has mean zero
and standard deviation 1. The standardized residuals depend on
An alternative unbiased estimate of
where
Using
which we term the internally studentized residual. Using teh other unbiased estimate, we get:
which is a monotonic transformation of
The externally standardized residuals follow a t-distribution with n - p - 2 degrees of freedom, but the internally standardized residuals do not. However, with a moderately large sample, these residuals should approximately have a standard normal distribution. The residuals are not strictly independently distributed, but with a large number of observations, the lack of independence may be ignored.
Graphical methods
Before fitting the model
Graphs plotted before fitting the model serve as exploratory tools. There are four categories of graphs:
1. One-dimensional graphs
One-dimensional graphs give a general idea of the distribution of each individual variable. One of the following graphs may be used:
- histogram
- stem-and-leaf display
- dot-plot
- box-plot
These graphs indicate whether the variable is symmetric, or skewed. When a variable is skewed, it should be transformed, generally using a logarithmic transformation. Univariate graphs also point out the presence of outliers in the variables. However, no observations should be deleted at this stage.
2. Two-dimensional graphs
We can take the variables in pairs and look at the scatter plots of
each variable versus each other variable in the data set. These
explore relationships between each pair of variables and identify
general patterns. These pairwise plots can be arranged in a matrix
format, known as the draftsman’s plot or the plot matrix. In simple
regression, we expect the plot of
Beyond these, there are rotation plots and dynamic graphs which serve as powerful visualizations of the data in more than 2 dimensions.
Graphs after fitting a model
The graphs after fitting a model help check the assumptions and assess the adequacy of the fit of a given model.
- Graphs checking linearity and normality assumptions
When the number of variables is small, the assumption of linearity can be checked by interactively and dynamically manipulating plots discussed in the previous section. However, this quickly becomes difficult with many predictor variables. Plotting the standardized residuals can help check the linearity and normality assumptions.
-
Normal probability plot of the standardized residuals: This is a plot of the ordered standardized residuals versus the normal scores. The normal scores are what we would expect to obtain if we take a sample of size
-
Scatter plots of the standardized residual against each of the predictor variables: Under the standard assumptions, the standardized residuals are uncorrelated with each of the predictor variables. If the assumptions hold, the plot should be a random scatter of points.
-
Scatter plot of the standardized residual versus the fitted values: Under the standard assumptions, the standardized residuals are also uncorrelated with the fitted values. Hence, this plot should also be a random scatter of points.
-
Index plot of the standardized residuals: we display the standardized residuals versus the observation number. If the order in which the observations were taken is immaterial, this plot is not needed. However, if the order is important, a plot of the residuals in serial order may be used to check the assumption of the independence of the errors.
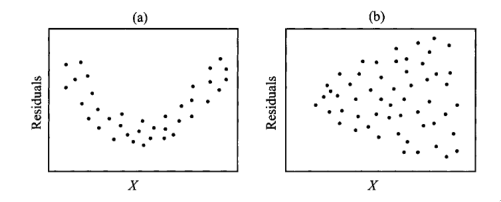
Figure 4: Scatter plots of residuals: (a) shows nonlinearity, and (b) shows heterogeneity
References
, Chatterjee and Hadi, n.d., @james2013introduction