Theory Of Computation
Introduction
Finite automata are a useful model for many kinds of important software and hardware. Automatas are found in compilers, software for designing digital circuits, and many more systems.
Grammars provide useful models when designing software that processes data with a recursive structure. The compiler’s parser deals with recursively nested features. Regular Expressions also denote the structure of data, especially in text strings.
The study of automata addresses the following questions:
- What can a computer do?
- What can a computer do efficiently?
Automata theory also provides a tool for making formal proofs, of both the inductive and deductive type.
Formal Proofs
Here the more common proof requirements are here:
- Proving set equivalence: we can approach this by rephrasing it into
an iff statement.
- Prove that if
xis inE, thenxis inF. - Prove that if
xis inF, thenxis inE.
- Prove that if
Inductive Proofs
Suppose we are given a statement
- The basis: where we show
- The inductive step: where we show if
Structural Inductions
We can sometimes prove statements by construction. This is often the
case with recursively defined structures, such as with trees and
expressions. This works because we the recursive definition is invoked
at each step, so we are guaranteed that at each step of the
construction, the construction
Automata Theory
Definitions
- alphabet
- An alphabet is a finite, nonempty set of symbols. E.g.
- string
- A string is a finite sequence of symbols chosen from some
alphabet. For example,
- Powers
- Concatenation
- Problem
- a problem is the question of deciding whether a given string is a member of some particular language.
Finite Automata
An automata has:
- a set of states
- its “control” moves from state to state in response to external inputs
A finite automata is one where the automaton can only be in a single state at once (it is deterministic). Non-determinism allows us to program solutions to problems using a higher-level language.
Determinism refers to the fact that on each input there is one and only one state to which the automaton can transition from its current state. Deterministic Finite Automata is often abbrieviated with DFA.
Deterministic Finite Automata
A dfa consists of:
- A finite set of states, often denoted
- A finite set of input symbols, often denoted
- A transition function that takes as arguments a state and an input
symbol and returns a state, often denoted
- A start state, one of the states in
- A set of final or accepting states
In proofs, we often talk about a DFA in “five-tuple” notation:
Simpler Notations
The two preferred notation for describing automata are:
- transition diagrams
- a graph
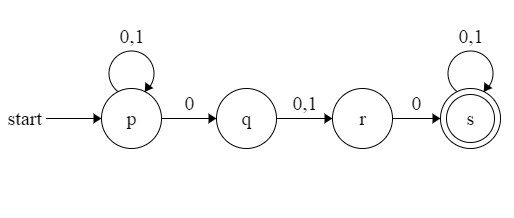
- transition table
- a tubular listing of the
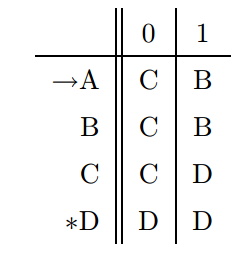
Language of a DFA
We can define the language of a DFA
The language of
Extending Transition Function to Strings
Basis:
Induction:
Nondeterministic Finite Automata
A NFA has can be in several states at once, and this ability is expressed as an ability to “guess” something about its input. It can be shown that NFAs accept exactly the regular languages, just as DFAs do. We can always convert an NFA to a DFA, although the latter may have exponentially more states than the NFA.
Definition
An NFA has:
- A finite set of states
- A finite set of input symbols
- A starting state
- A set of final states
- A transition function that takes a state in
The Language of an NFA
if
That is,
The Equivalence of DFA and NFA

Finite Automata with Epsilon-Transitions
Transitions on ε, the empty string, allow NFAs to make a transition spontaneously. This is sometimes referred to as ε-NFAs, and are closely related to regular expressions.
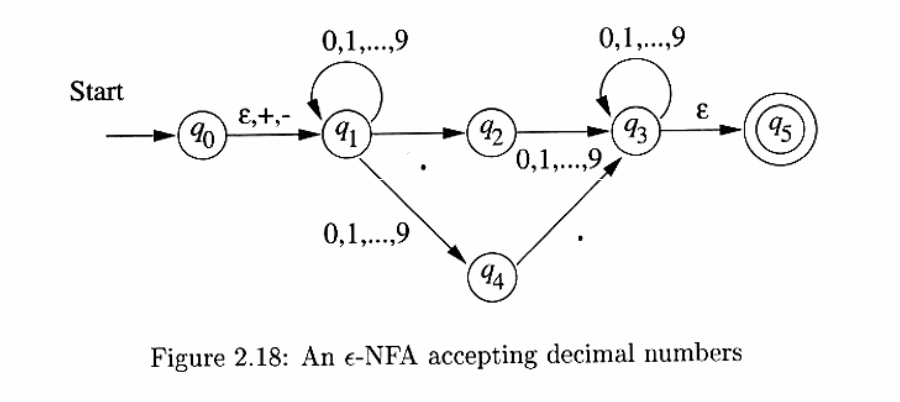
Of particular interest is the transition from
Epsilon-Closures
We ε-close a state
ε-closure allows us to explain easily what the transitions of an
ε-NFA look like when given a sequence of (non-ε) inputs. Suppose
that
BASIS:
INDUCTION: Suppose
Eliminating ε-Transitions
Given any ε-NFA
Let
- Let
- Compute
- Then
- Let
Regular Expressions
Regular expressions may be thought of as a “programming language”, in which many important applications like text search applications or compiler components can be expressed in.
Regular expressions can define the exact same languages that various forms of automata describe: the regular languages. Regular expressions denote languages. We define 3 operations on languages that the operators of regular expressions represent.
- The union of two languages
- The concatenation of languages
- The closure (or star, or Kleene closure) is denoted
We can describe regular expressions recursively. For each expression
BASIS:
- The constants
- If
INDUCTION:
Precedence of regular expression operators
The precedence in order of highest to lowest, is:
- star
- dot (note that this operation is associative)
- union (
Equivalence of DFA and Regular Expressions
We show this by showing that:
- Every language defined by a DFA is also defined by a regular expression.
- Every language defined by a regular expression is also defined by a $\epilon$-NFA, which we have already shown is equivalent to a DFA.
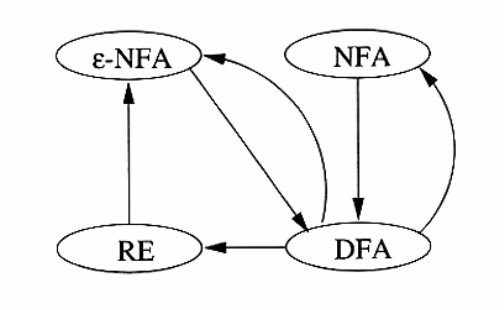
From DFA to Regular Expression
We can number the finite states in a DFA
Let
BASIS:
- An arc from node (state)
- A path of length
If
- If there is no such symbol
- If there is exactly one such symbol
- If there are symbols
In case (a), the expression becomes
INDUCTION: Suppose there is a path from state
- The path does not go through state
- The path goes through state
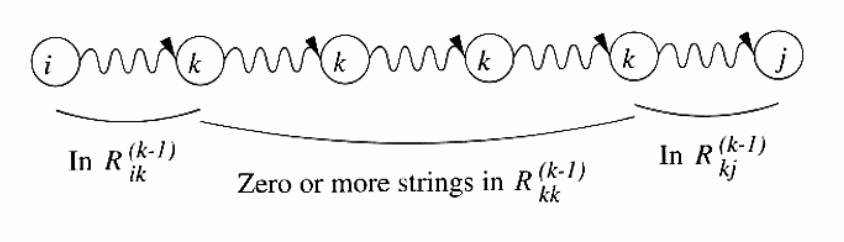
Then the set of labels for all paths of this type is represented by
the regular expression
We can compute
Converting DFAs to regular expressions by eliminating states
The above method of conversation always works, but is expensive.
The approach introduced here avoids duplicating work at some points,
by eliminating states. If we eliminate a state
Hence, we can construct a regular expression from a finite automaton as follows:
- For each accepting state
- If
- If the start state is also an accepting state, then we must perform
a state-elimination from the original automaton that gets rid of
every state but the start state, leaving a one-state automaton,
which accepts
Converting regular expressions to automata
We can show every language defined by a regular expression is also
defined by a finite automaton, and we do so by converting any regular
expression
- Exactly one accepting state
- No arcs into initial state
- No arcs out of the accepting state
The proof is conducted by structural induction on R, following the recursive definition of regular expressions.
The basis of the induction involves constructing automatons for
regular expressions (a)
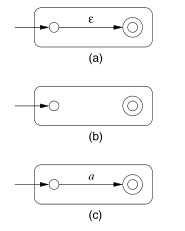
The inductive step consists of 4 cases: (a) The expression is
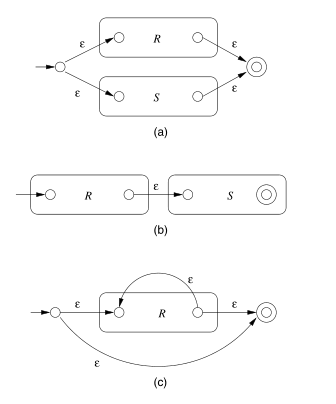
The automaton for
Algebraic law for regular expressions
- commutativity
- associativity
- distributive
Discovering laws for regular expressions
The truth of a law reduces to the question of the equality of two languages. We show set equivalence: a string in one language must be in another, and vice-versa.
Properties of Regular Languages
Regular languages exhibit the “closure” property. These properties let us build recognizers for languages that are constructed from other languages by certain operations. Regular languages also exhibit “decision properties”, which allow us to make decisions about whether two automata define the same language. This means that we can always minimize an automata to have as few states as possible for a particular language.
Pumping Lemma
We have established that the class of languages known as regular languages are accepted by DFAs, NFAs and by $ε$-NFAs.
However, not every language is a regular language. An easy way to see this is that the number of languages is infinite, but DFAs have finite number of states, and are finite.
The pumping lemma lets us show that certain languages are not regular.
Let
- For all
That is, we can always find a non-empty string
Note that there has been other ways to prove irregularity of languages.
Closure of Regular Languages
If certain languages are regular, then languages formed from them by certain operations are also regular. These are referred to as the closure properties of regular languages. Below is a summary:
- Union of 2 regular languages
- Intersection of 2 regular languages
- Complement of 2 regular languages
- Difference of 2 regular languages
- Reversal of a regular language
- Closure (star) of a regular language
- The concatenation of regular languages
- A homomorphism (substitution of strings for symbols) of a regular language
- The inverse homomorphism of a regular language
The above are all regular.
Context-free Grammars and Languages
Context-free languages are a larger class of languages, that have context-free grammars. We show how these grammars are defined, and how they define languages.
Context-free grammars are recursive definitions. For example, the context-free grammar for palindromes can be defined as:
There are four important components in a grammatical description of a language:
- There is a finite set of symbols that form the strings of the language. These alphabets are called the terminals, or terminal symbols.
- There is a finite set of variables, or nonterminals or syntactic
categories. Each variable represents a language. In the language
above, the only variable is
- One of the variables represents the language being defined, called the start symbol.
- There is a finite set of productions or rules that represent the
recursive definition of a language. Each production rule consists:
- A variable that is being defined by the production (called the head).
- The production symbol
- A string of zero or more terminals and variables.
We can represent any CFG as these 4 components, we denote CFG
Derivations using a Grammar
We can apply the productions of a CFG to infer that certain strings are in the language of a certain variable.
The process of deriving strings by applying productions from head to
body requires the definition of a new relation symbol,
We may extend the
Leftmost and Rightmost Derivations
In order to restrict the number of choices we have in deriving a
string, it is often useful to require that at each step, we replace
the leftmost variable by one of its production bodies. Such a
derivation is called a leftmost derivation. Leftmost derivations are
indicated with
Similarly, it is possible to require that at each step the rightmost
variable is replaced by one of its bodies. These are called rightmost
derivations. These are similarly denoted
The language of a Grammar
If
Sentential Forms
Derivations from the start symbol produce strings that have a special role. These are called sentential forms. We also denote left-sentential and right-sentential forms for leftmost derivations and rightmost derivations respectively.
Parse Trees
There is a tree representation of derivations, that clearly show how symbols of a terminal string are grouped into substrings, each of which belongs to the language of one of the variables of the grammar. This tree is the data structure of choice when representing the source of a program.
Construction
The parse trees for a CFG
- Each interior node is labeled by variable in
- Each leaf is labeled by either a variable, a terminal, or
- If an interior node is labeled
The yield
The yield of the tree is the concatenation of the leaves of the parse
tree from the left. This yield is a terminal string (all leaves are
labeled either with a terminal or with
Inferences and derivations
The following statements are equivalent:
- The recursive inference procedure determines that terminal string
- There is a parse tree with root
We can prove these equivalences using the following arcs:
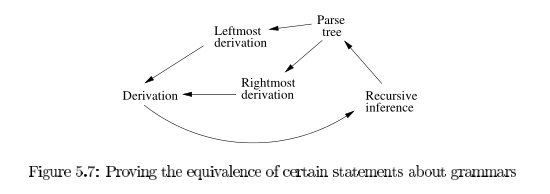
Linear Grammars
Right linear grammars have all the productions of form:
Every regular language can be generated by some right-linear grammar.
Suppose
- For
- We also have productions
We can prove by induction on
TODO Ambiguous Grammars
Chomsky Normal Form
Chomsky normal form is useful in giving algorithms for working with context-free grammars. A context-free grammar is in Chomsky normal form if every rule is of the form:
weher
Any context-free language is generated by a context-free grammar in Chomsky normal form. This is because we can convert any grammar into Chomsky normal form.
Pushdown Automata
Pushdown automata are equivalent in power to context-free grammars This equivalence is useful because it gives us two options for proving that a language is context-free. Certain languages are more easily described in terms of recognizers, while others aremore easily described in terms of generators.
Definition
It is in essence a nondeterministic finite automaton with ε-transitions permitted, with one additional capability: a stack on which it can store a string of “stack symbols”.
We can view the pushdown automaton informally as the device suggested below:
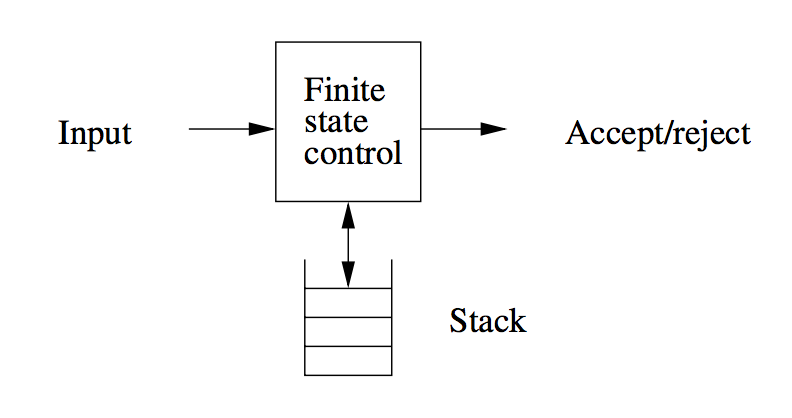
A “finite-state-control” reads inputs, one symbol at a time. The automaton is allowed to observe the symbol at the top of the stack, and to base its transition on its current state. It :
- Consumes from the input the symbol it uses in the transition. If ε is used for the input, then no input symbol is consumed.
- Goes to a new state
- Replaces the symbol at the top of the stack by any string. This corresponds to ε, which corresponds to a pop of the stack. It could also replace the top symbol by one other symbol. Finally the top stack symbol could be replaced by 2 or more symbols, which has the effect of changing the top stack symbol, and pushing one or more new symbols onto the stack.
Formal Definition
We can specify a PDA
The formal definition of a PDA contains no explicit mechanism to allow the PDA to test for an empty stack. The PDA is able to get the same effect by initially placing a special symbol $ on the stack. If it sees the $ again, it knows that the stack effectively is empty.
We can also draw transition diagrams for PDAs. An example is shown below.
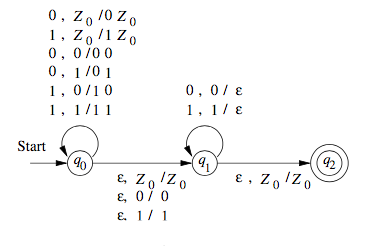
Instantaneous Descriptions
We represent the configuration of a PDA by a triple
Conventionally, we show the top of the stack at the left, and the bottom at the right. This triple is called the instantaneous description, or ID, of the pushdown automaton.
For finite automata, the
We use
The Languages of PDAs
The class of languages for PDAs that accept by final state and accept by empty stack are the same. We can show how to convert between the two.
Acceptance by Final State
Let
for some state
Acceptance by Empty Stack
Let
From Empty Stack to Final State
Theorem:
If
Proof:
We use a new symbol
We also use a new start state
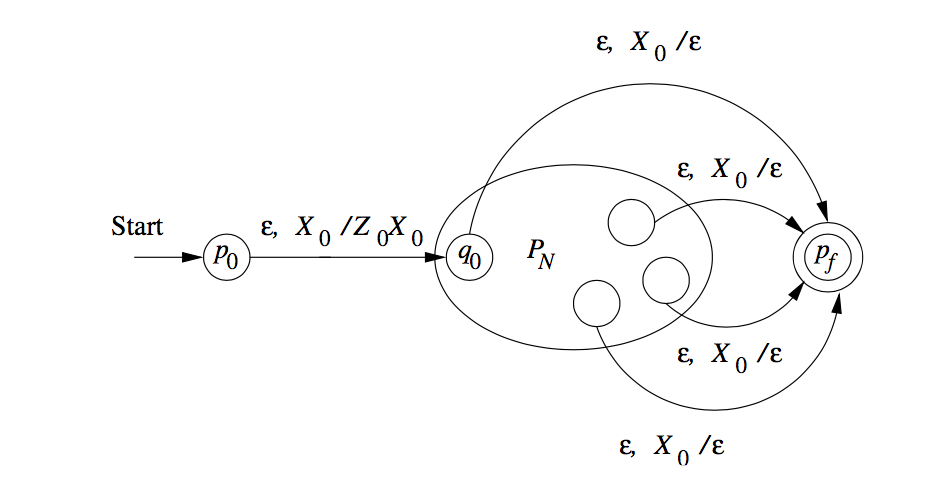
Hence, we can specify
- For all states
From Final State to Empty Stack
Whenever
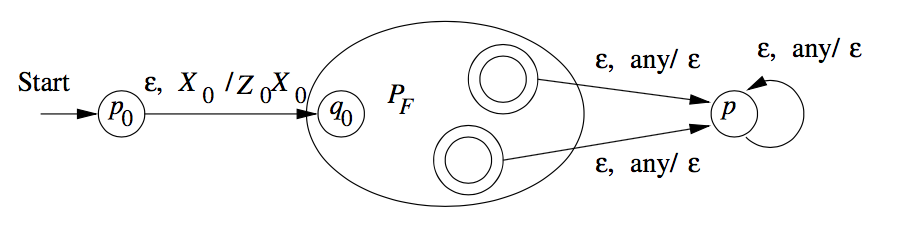
To avoid simulating a situation where
That is
- For all states
- For all accepting states
- For all stack symbols
Equivalence of CFG and PDA
Let
The PDA
The PDA
- Place the marker symbol $ and the start variable on the stack
- Repeat:
- If the top of stack is a variable symbol
- If the top of stack is a terminal symbol
- If the top of stack is the symbol $, enter the accept state.
- If the top of stack is a variable symbol
Now we prove the reverse direction. We have a PDA
For each pair of states
First, we simplify the task by modifying P slightly to give it the following three features.
- It has a single accept state,
- It empties its stack before accepting.
- Each transition either pushes a symbol onto the stack (a push move) or pops one off the stack (a pop move), but it does not do both at the same time.
Giving
To design
First, we simplify our task by modifying
Deterministic Pushdown Automata
DPDAs accept a class of languages between the regular languages and the CFLs.
We can easily show that DPDAs accept all regular languages by making it simulate a DFA (ignoring the stack).
While DPDAs cannot represent all CFLs, it is able to represent languages that have unambiguous grammars.
Properties of Context-Free Languages
Simplification of CFG
The goal is to reduce all CFLs to Chomsky Normal Form. To get there, we must make several preliminary simplifications, which are useful in their own ways.
-
Elimination of useless symbols
- Remove all non-reachable symbols: starting from
- Remove all non-generating symbols: for each symbol, check if the
symbol can ever generate a terminating string. If not, remove
it. Example:
- It is important to remove non-generating symbols first, because it can lead to more non-reachable symbols.
- Remove all non-reachable symbols: starting from
-
Removal of unit productions
-
Unit productions look like
-
To eliminate unit productions, we substitute the unit symbol into the production.
-
-
Removal of
- Start from any symbol, remove the
- Eliminate until no more $ε$-productions.
- When an $ε$-production is eliminated from a symbol, it does not need to be reapplied if it appears again in the same symbol.
- Start from any symbol, remove the
-
Conversion to Chomsky Normal Form
After performing the preliminary simplifications, we can then:
- Arrange that all bodies of length 2 or more consist only of variables
- Break bodies of length 3 or more into a cascade of productions
Pumping Lemma for CFLs
In any sufficiently long string in a CFL, it is possible to find at most 2 short, nearby substrings, that we can pump in tandem. First, we use several results, that we will state below.
- Conversion to CNF converts a parse tree into a binary tree.
- For a CNF grammar
Let
- $ vx ≠ ε$
- For all
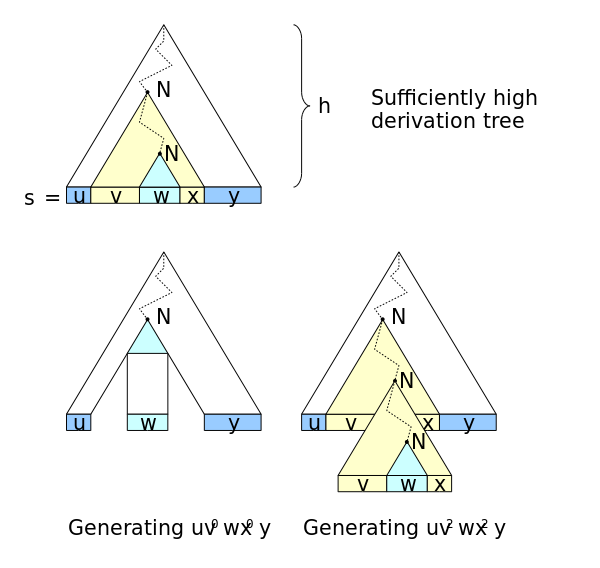
If
Closure Properties of CFLs
First, we introduce the notion of substitutions. Let
If
The substitution theorem states that if we can find a substitution
function
CFLs are closed under:
- Union
- Concatenation
- Closure, and positive closure (asterisk and plus)
- Homomorphism
These are the base closure properties. CFLs are also closed under reversal. We can prove this by constructing a grammar for the reversed CFL.
CFLs are not closed under intersection. However, CFLs are closed under the operation of “intersection with a regular language”. To prove this, we use the PDA representation of CFLs, and FA representation of regular languages. We can run the FA in parallel with the PDA.
CFLs are also closed under inverse homomorphism. The proof is similar to that of regular languages, but using a PDA, but is more complex because of the stack introduced in the PDA.
Decision Properties of CFLs
First, we consider the complexity of converting from a CFG to a PDA,
and vice versa. Let
Below, we list algorithms linear in the size of the input:
- Converting a CFG to a PDA
- Converting a PDA that accepts by final state to one that accepts by empty stack
- Converting a PDA that accepts by empty stack to one that accepts by final state
The running time of conversion from a PDA to a grammar is much more
complex. The upper bound on the number of states and stack symbols is
However, we can break the pushing of a long string of stack symbols
into a sequence of at most
Running Time of Conversion to CNF
- Detecting reachable and generating symbols can be done in
- Constructing unit pairs and eliminating unit productions takes
- Replacing terminals by variables in production bodies takes
- Breaking production bodies of length 3 or more takes
However eliminating $ε$-productions is tricky. If we have a production
body of length
In all, converting to CNF form is a
Testing for emptiness of CFL
This is equivalent to testing if
We maintain an array indexed by variable, which tells whether or not we have established that a variable is generating.For each variable there is a chain of all the positions in which the variable occurs (solid lines). The dashed lines suggest links from the productions to their counts.
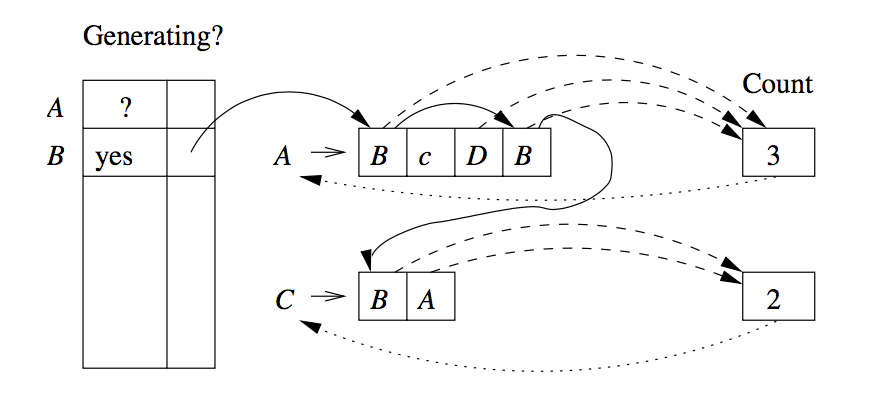
For each production, we count the number of positions holding variables whose ability to generate is not yet accounted for. Each time the count for a head variable reaches 0, we put the variable on a queue of generating variables whose consequences need to be explored.
This algorithm takes
- There are at most
- Initialization of the links and counts can be done in
- When we discover a production has count 0:
- Discover a production has count
- work done when visiting the production bodies that have the head
variable
- Discover a production has count
Testing Membership in a CFL
First, we can easily see that algorithms exponential in
Fortunately, more efficient techniques exist, based on the idea of dynamic programming. Once such algorithm is the CYK Algorithm.
We construct a triangular table, and begin the fill the table
row-by-row upwards. The horizontal axis corresponds to the positions
of the string
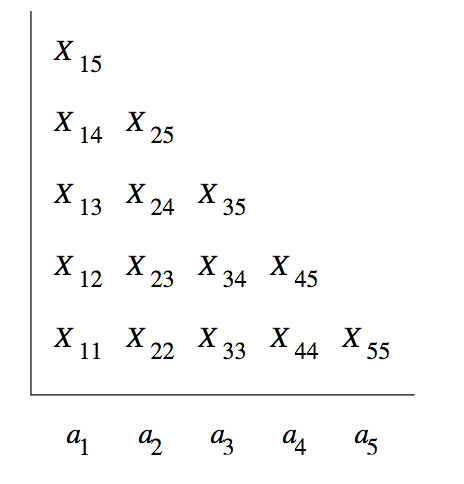
It takes
The algorithm for computing
BASIS: We compute the first row as follows. Since the string beginning
and ending at position
INDUCTION: To compute
For
Finding such variables
Turing Machines
We now look at what languages can be defined by any computational device. The Turing Machine is an accurate model for what any physical computing device is capable of doing. More technically, turing machines facilitate proving everyday questions to be undecidable or intractable.
Turing machines are finite automata with a tape of infinite length on which it may read and write data. The machine consists of a finite control, which can be in any of a finite set of states. There is a tape divided into squares or cells; each cell can hold any one of a finite number of symbols.
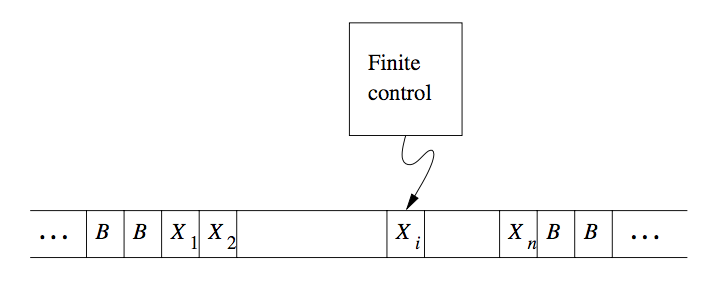
Figure 1: A Turing Machine
Initially, the input, which is a finite-length string of symbols chosen from the input alphabet, is placed on the tape. All other tape cells, extending infinitely to the left and right, initially hold a special symbol called the blank. The blank is a tape symbol, but not an input symbol, and there may be other tape symbols.
There is a tape head that is always positioned at one of the tape cells. The Turing machine is said to be scanning that cell.
A move of the Turing machine is a function of the state of the finite control and the tape symbol scanned.
- Change state: The next state optionally may be the same as the current state.
- Write a tape symbol in the cell scanned. This tape symbol replaces whatever symbol was in that cell.
- Move the tape head left or right.
Formal Notation
The formal notation used for a Turing Machine (TM) is by a 7-tuple:
where:
- Q
- The finite set of states of the finite control
- Σ
- The finite set of input symbols
- Γ
- The complete set of tape symbols. Σ is a subset of Γ.
- δ
- The transition function. The arguments of
- q_0
- The start state, a member of Q
- B
- the blank symbol, in Γ but not Σ
- F
- the set of final or accepting states
Instantaneous Descriptions
We use the string
- The tape head is scanning the $i$th symbol from the left.
We describe moves of a Turing machine
There are 2 important exceptions, when
Transition Diagrams
Turing machines can be denoted graphically, as with PDAs.
An arc from state
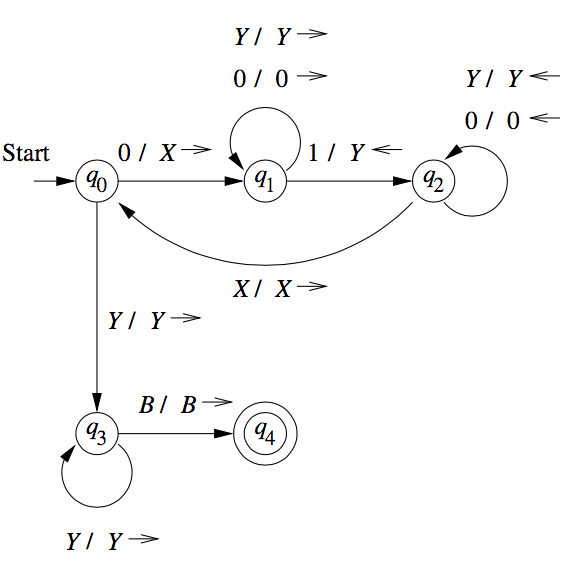
Figure 2: Transition diagram for TM accepting
The Language of a TM
Turing machines and halting
A TM halts if it enters a state
Languages that halt eventually, regardless of whether they accept, are called recursive. If an algorithm to solve a given problem exists, then we say the problem is decidable, so TMs that always halt figure importantly into decidability theory.
Programming Techniques for Turing Machines
Storage in the State
We can use the finite control not only to represent a position in the
“program” of a TM, but to hold a finite amount of data. We extend
the state as a tuple
Multiple Tracks
One can also think of the tape of a Turing machine as composed of several tracks. Each track can hold one symbol, and the tape alphabet of the TM consists of tuples, with each component for each “track”. A common use of multiple tracks is to treat one track as holding the data, and another track as holding a mark. We can check off each symbol as we “use” it, or we can keep track of a small number of positions within the data by only marking these positions.
Subroutines
A Turing machine subroutine is a set of states that perform some useful process. This set of states includes a start state and another state to pass control to whatever other set of states called the subroutine. Since the TM has no mechanism for remembering a “return address”, that is, a state to go to after it finishes, should our design of a TM call for one subroutine to be called from several states, we can make copies of the subroutine, using a new set of states for each copy. The “calls” are made to the start states of different copies of the subroutine, and each copy “returns” to a different state.
Multitape Turing Machines
The device has a finite control (state), and some finite number of tapes. Each tape is divided into cells, and each cell can hold any symbol of the finite tape alphabet.
Initially, the head of the first tape is at the left end of the input, but all other tape heads are at some arbitrary cell.
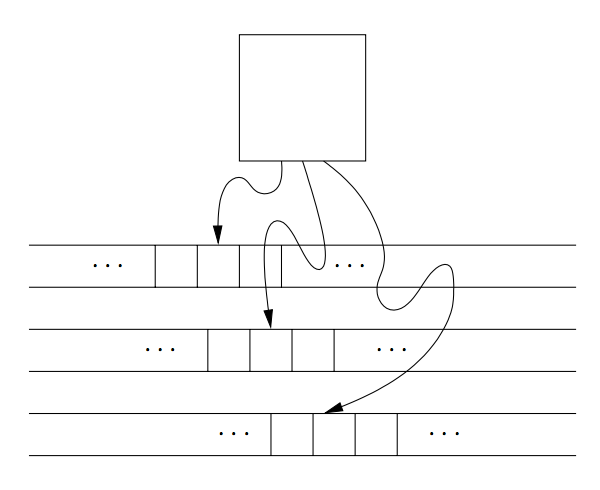
Figure 3: A multitape Turing machine
A move on the multitape TM depends on the state and symbol scanned by each of the tape heads. On each move:
- the control enters a new state, which could be the same as a previous state.
- On each tape, a new tape symbol is written on the cell scanned. This symbol could be the same as the previous symbol.
- Each tape head makes a move, which can be either left, right or stationary.
Equivalence of one-tape and multitape TMs
Suppose language
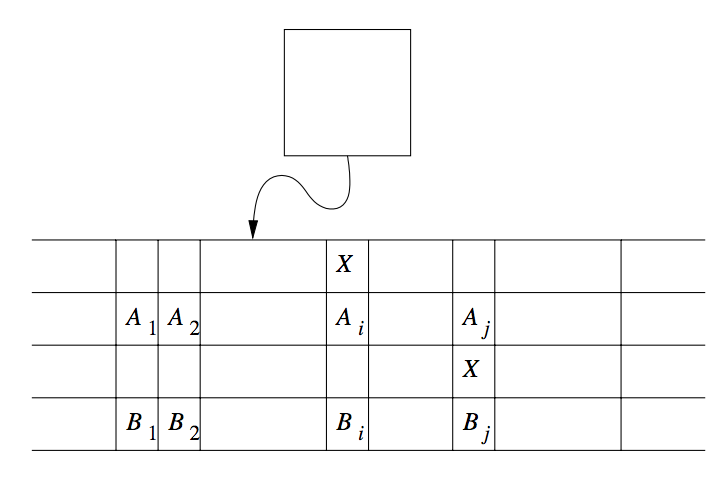
Figure 4: Simulation of two-tape Turing machine by a one-tape Turing machine
To simulate a move of
The time taken by the one-tape TM
Non-deterministic Turing Machines
A NTM differs from the deterministic variety by having a transition
The NTM can choose at each step any of the triples to be the next
move. We can show that NTM and TM are equivalent. The proof involves
showing that for every NTM
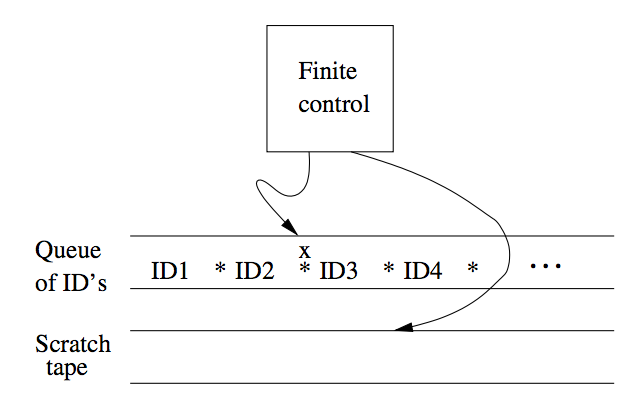
Figure 5: Simulation of NTM by a DTM
To process the current ID,
- However, if the state is not accepting, and the state-symbol
combination has
This can be viewed as a breadth-first search on all possible IDs reached.
Restricted Turing Machines
Turing Machines with Semi-infinite Tapes
We can assume the tape to be semi-infinite, having no cells to the left of the initial head position, an still retain the full power of TMs.
The trick behind the construction is to use two tracks on the
semi-infinite tape. The upper track represents the cells of the
original TM that are at or to the right of the initial head position,
but in reverse order. The upper track represents

Another restriction we make is to never write a blank. This combined with the semi-infinite tape restriction means that the tape is at all times a prefix of non-blank symbols followed by an infinity of blanks.
We can construct an equivalent TM
Multistack Machines
A $k$-stack machine is a deterministic PDA with
- The state of the finite control
- The input symbol read, which is chosen from the finite input alphabet.
Each move allows the multistack machine to:
- Change to a new state
- Replace the top symbol of each stack with a string of zero or more stack symbols.
If a language is accepted by a TM, it is also accepted by a two-stack machine.
Counter Machines
Counter machines have the same structure as the multistack machine, but in place of each stack is a counter. Counters holdd any non-negative integer, but we can only distinguish between zero and non-zero counters. That is, the move of the counter machine depends on its state, input symbol, and which, if any, of the counters are zero.
Each move can:
- Change state
- Add or subtract 1 from any of its counters independently
A counter machine can be thought of as a restricted multistack machine, where:
- There are only 2 stack symbols, which is the bottom-of-stack marker
- We may replace
- We may replace
We observe the following properties:
- Every language accepted by a counter machine is recursively enumerable.
- Every language accepted by a one-counter machine is a CFL. This is made immediately obvious by considering that it is a one-stack machine (a PDA).
- Every language accepted by a two-counter machine is RE.
The proof is done by showing that three counters is enough to simulate a TM, and that two counters can simulate three counters.
Proof outline: Suppose there are
Turing Machines and Computers
- A computer can simulate a Turing machine, and
- A Turing machine can simulate a computer, and can do so in an amount of time that is at most some polynomial in the number of steps taken by the computer
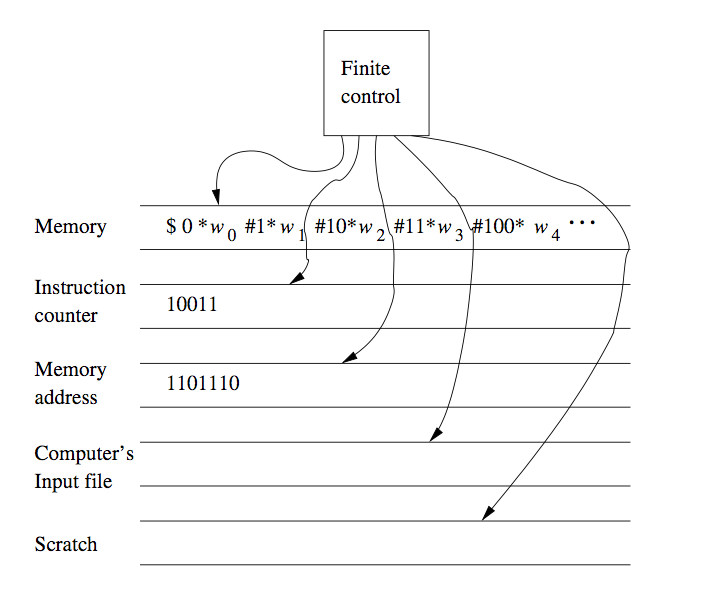
We can prove the latter by using a TM to simulate the instruction cycle of the computer, as follows:
- Search the first tape for an address matching the instruction number on tape 2.
- Examine the instruction address value, if it requires the value of some address, that address is part of the instruction. Mark the position of the instruction using a second tape, not shown in the picture. Search for the memory address on the first tape, an dcopy its value onto tape 3, the tape holding the memory address
- Execute the instruction. Examples of instructions are:
- Copying values to some other address
- Adding value to some other address
- The jump instruction
Runtime of Computers vs Turing Machines
Running time is an important consideration, because we want to know what can be computed with enough efficiency. We divide between tractable and intractable problems, where tractable problems can be solved efficiently.
Hence, we need to assure ourselves that a problem can be solved in polynomial time on a typical computer, can be solved in polynomial time on a TM, and conversely.
A TM can simulate
To resolve this issue, one can assert that words retain a maximum length. We take another approach, imposing the restriction that instructions may use words of any length, but can only produce words one bit longer than its arguments.
The prove the polynomial time relationship, we note that after
Hence, if a computer:
- Has only instructions that increase the maximum word length by at most 1, and
- Has only instructions that a multitape TM can perform on wordsd of
length
the Turing machine can simulate