Probabilistic Graph Models
Motivation
Most tasks require a person or an automated system to reason: to take the available information and reach conclusions, both about what might be true in the world and about how to act. Probabilistic graphical models represent a general framework that can be used to allow a computer system to reason.
Using this approach of declarative representation, we construct, within the computer, a model of the system about which we would like to reason. This model encodes our knowledge of how the system works in a computer-readable form. This representation can then be manipulated by various algorithms that can answer questions based on the model.
The key property of a declarative representation is the separation of knowledge and reasoning. The representation has its own clear semantics, separate from the algorithms that one can apply to it. Thus, we can develop a general suite of algorithms that apply any model within a broad class, whether in the domain of medical diagnosis or speech recognition. Conversely, we can improve our model for a specific application domain without having to modify our reasoning algorithms constantly.
Uncertainty is a fundamental quantity in many real-world situations. To obtain meaningful conclusions, we need to reason not just about what is possible, but what is probable.
The calculus of probability theory provides us with a formal framework for considering multiple outcomes and their likelihood. This frameworks allows us to consider options that are unlikely, yet not impossible, without reducing our conclusions to content-free lists of every possibility.
One finds that probabilistic models are very liberating. Where in a more rigid formalism, we might find it necessary to enumerate every possibility, here we can often sweep a multitude of annoying exceptions and special cases under the probabilistic rug, by introducing outcomes that roughly correspond to “something unusual happens”. This type of approximation is often inevitable, as we can only rarely provide a deterministic specification of the behaviour of a complex system. Probabilistic models allow us to make this explicit, and therefore provide a model that is more faithful to reality.
Graphical Representation
Probabilistic graphical models use a graph-based representation as the basis for compactly encoding a complex distribution over a high-dimensional space. In this graphical representation, the nodes correspond to the variables in our domain, and the edges correspond to direct probabilistic interactions between them.
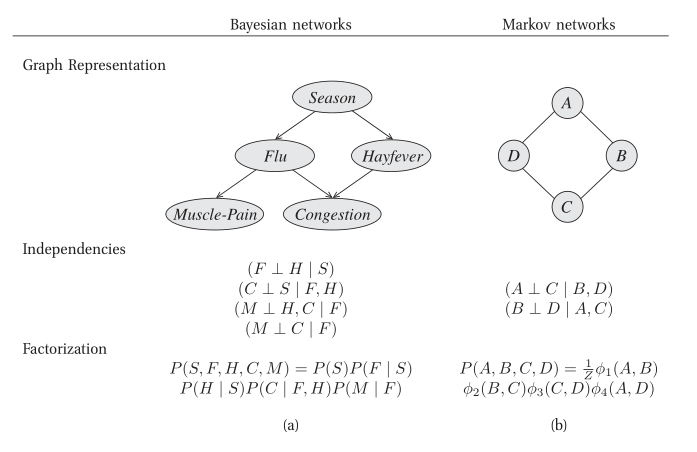
Figure 1: Different perspectives on probabilistic graphical models
Bayesian Networks
The goal is to represent a joint distribution
The compact representations explored are based on two key ideas: the representation of independence properties of the distribution, and the use of an alternative parameterization that allows us to exploit these fine-grained independencies.
Bayesian networks build on the same intuitions as the naive Bayes
model by exploiting conditional independence properties of the
distribution in order to allow a compact and natural representation.
The core of the Bayesian network representation is the directed graph
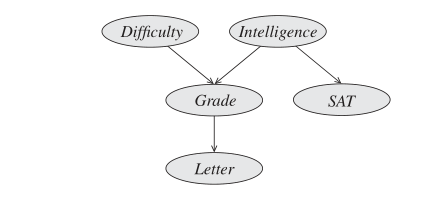
Figure 2: Example of a Bayesian Network graph
This graph
- as a data structure that provides the skeleton for representing a joint distribution compactly in a factorized way;
- as a compact representation for a set of conditional independence assumptions about a distribution.
These two views, are in a strong sense, equivalent.
Bayesian Network Semantics
We can formally define the Bayesian network structure as follows:
Let
In other words, the local independencies state that each node
The formal semantics of a Bayesian network graph is as a set of
independence assertions. On the other hand, our representation was a
graph annotated with conditional probability distributions (CPDs).
Here, we show that these two definitions are, in fact equivalent. A
distribution
I-Maps
Let
Now, we need to show that
Let
Now, we can say we need to show that
For
I-Map to Factorization
A BN structure
Consider the joint distribution
This decomposition requires no assumptions. We may however be able to apply our conditional independence assumptions induced from the BN.
We say that a distribution
This equation is called the chain rule for BNs. The individual factors
We can now show that if
Proof:
Assume, without loss of generality, that
Now consider one of the factors
where
Applying this transformation to all of the factors in the chain rule decomposition gives the desired result.
Factorization to I-map
This is simple to prove, by manipulation of probabilities.
Independencies in Graphs
Dependencies and independencies are crucial for understanding the behaviour of a distribution. Independency properties are also important for answering queries: they can be exploited to reduce substantially the computational cost of inference. Therefore, it is important that our representations make these properties clearly visible both to a user and to algorithms that manipulate the BN data structure.
The immediate question that arises is whether there exist independence
properties that we can read off directly from
D-separation
We want to be able to guarantee that an independence
Direct Connection
If
Indirect Connection
Consider a 3-node network where
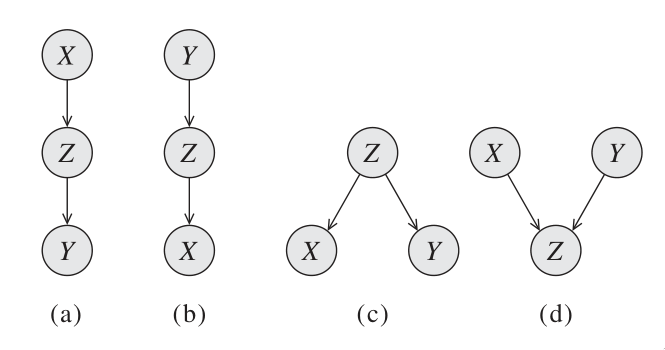
We say that Q, W are d-separated when variables
- Casual trail
- Evidential trail
- Common cause
- Common effect
Consider the general trail
- Whenever we have a v-structure
- no other node along the trail is in
Let
This set is also called the set of global Markov independencies. These
independencies are precisely those that are guaranteed to hold for
every distribution over
A nice tutorial on d-separation can be found here.
Markov Blanket
Consider a joint distribution
We observe that any factor
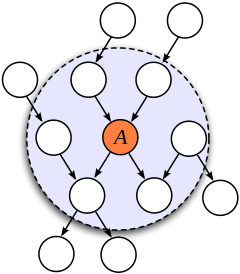
Figure 3: An illustration of the Markov Blanket. (Source)
Soundness and Completeness
- Soundness
- If a distribution
- Completeness
- If we have 2 variables
- Faithful
- A distribution
The notion of faithfulness is the converse of our notion of soundness. However, it can be shown that this desirable property of faithfulness is false.
We can, however, adopt a weaker but useful definition of completeness:
If
Using this definition, we can show that If
This completeness result tells us that our definition of
In fact, for almost all distributions
An algorithm for d-separation
There is a linear-time (in the size of the graph) algorithm for determining the set of d-separations. The algorithm has 2 phases:
- Traverse the graph bottom up, from the leaves to the roots, marking
all nodes that are in
- Traverse breadth-first from
A node is blocked if:
- it is the “middle” node in a v-structure and unmarked in phase I, or
- It is not a middle node and is in
If the BFS gets us from

I-equivalence
The notion of
One important implication of this perspective is the observation that very different BN structures can actually be equivalent, in that they encode the same set of conditional independence assumptions.
This brings us to the notion of I-equivalence:
Two graphs
This notion implies that any distribution
From Distributions to Graphs
Given a distribution
Minimal I-maps
One approach to finding a graph that represents a distribution
A graph
To obtain a minimal I-map we simply follow a natural algorithm that arises through the factorization theorem. Note that the minimal I-map is not necessarily unique in this construction.

Minimal I-maps fail to capture all the independencies that hold in the
distribution. Hence, that
Perfect Maps
A graph
Unfortunately, not every distribution has a perfect map. There exists an algorithm for finding the DAG representing the P-map for a distribution of a P-map if it exists, but is quite involved. See Koller, Friedman, and Bach, n.d..
Undirected Graphical Models
(The bulk of the material is from Murphy’s book Murphy, n.d.)
For some domains, being forced to choose a direction for the edges, as required by a DGM is awkward. For example, if we’re modelling an image, we might suppose that the neighbouring pixels are correlated. We may form a DAG model with a 2d lattice topology as such:
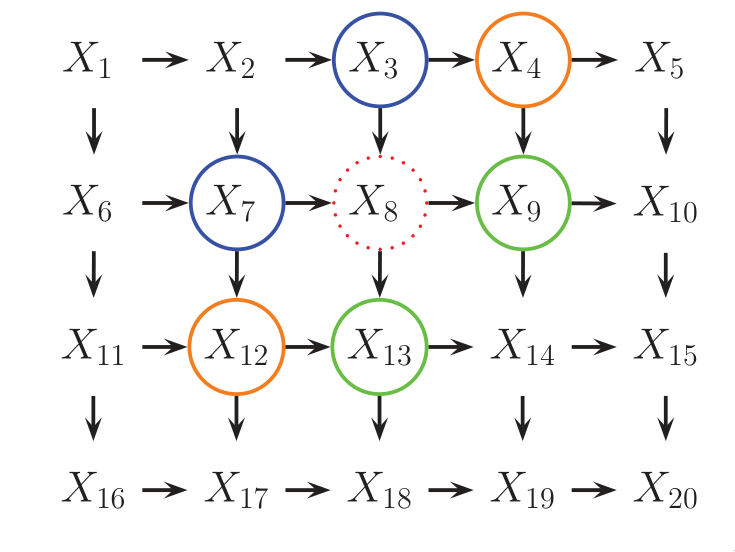
Figure 4: 2d lattice represented as a DAG.
However, representing the conditional probabilities in this way is
rather unnatural: the Markov blanket of node
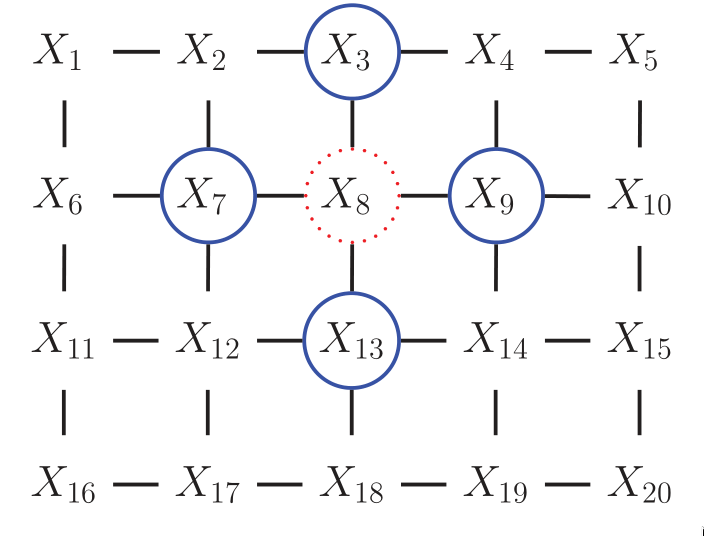
Figure 5: UGM representation of the lattice topology.
Conditional Independence Properties of UGMs
UGMs define CI relationships via simple graph separation as follows:
- global Markov property
- local Markov property
- pairwise Markov property
The global Markov property implies the local and pairwise Markov
properties. If
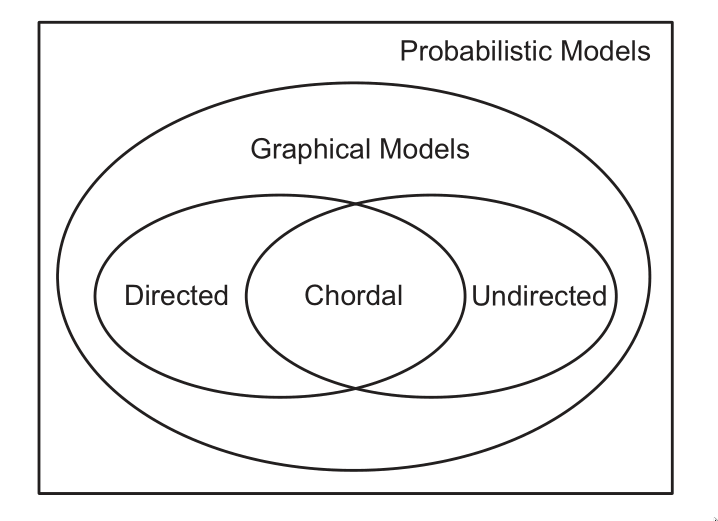
Representation Power
DGMs and UGMs can perfectly represent different set of distributions. The set of distributions that are perfectly represented by both DGMs and UGMs are termed chordal.
In general, CI properties in UGMs are monotonic, in the following
sense: if
If all the variables are collapsed in each maximal clique to make “mega-variables”, the resulting graph will be a tree if the distribution is chordal.
The Undirected alternative to d-separation
It is tempting tot simply convert the DGM to a UGM by dropping the orientation of the edges, but this is incorrect because a v-structure has different CI properties than the undirected chain. To avoid such incorrect CI statemnets, we can add edges between the “unmarreid” parents A and C, and then drop the arrows from the edges, forming in a connected undirected graph. This process is called moralization.
Moralization loses some CI information, and therefore we cannot used a moralized UGM to determine CI properties of the DGM.
Parameterization of MRFs
Since there is no topological ordering in an unordered graph,
A positive distribution
were
Connection between statistical physics
There is a model known as the Gibbs distribution, which can be written as follows:
where
Here we see that high probability states correspond to low energy configurations. We are also free to restrict the parameterization to the edges of the graph. A rather convenient formulation is the pairwise MRF.
Representing Potential Functions
If the variables are discrete, we can represent the potential or energy functions as tables of (non-negative) numbers, as with CPTs. However, the potentials are not probabilities, but rather a representation of relative “compatibility” or “happiness” between the different assignments.
A more general approach is to define the log potentials as a linear function of the parameters:
where
This is also known as the maximum entropy or log linear model.
Several popular probability models, such as the Ising model, Potts model and Hopfield networks, can be conveniently expressed as UGMs.
Parameter Estimation in UGMs
Consider an MRF in log-linear form:
where
Since MRFs are in the exponential family, we know that this function
is convex in
The derivative for the weights of a particular clique is given by:
The derivative of the log partition function wrt to
In the first term, we fix
Approximate methods for computing the MLEs of MRFs
When fitting a UGM there is (in general) no closed form solution for the ML or the MAP estimate of the parameters, so we need to use gradient-based optimizers. This gradient requires inference. In models where inference is intractable, learning is also intractable. This motivates computationally faster alternatives to ML/MAP estimation, such as pseudo likelihood, and stochastic maximum likelihood.

Figure 6: Stochastic maximum likelihood

Figure 7: Iterative Proportional Fitting
Conditional Random Fields (CRFs)
A CRF is a version of an MRF where all the clique potentials are conditioned on input features:
It can be thought of as a structured output extension of logistic regression. A log-linear representation of the potentials is often assumed.
The advantage of a CRF over a MRF is analogous to the advantage of a discriminative classifier over a generative classifier, where we don’t need to “waste resources” modeling things that we always observe, but instead model the distribution of labels given the data.
In the CRF, we can also make the potentials of the model be data-dependent. For example, we can make the latent labels in an NLP problem depend on global properties of the sentence.
However, CRF requires labeled training data, and are slower to train.