Jethro's Braindump

Imitation Learning

Behavioural Cloning

Behavioural cloning is a fancy name for supervised learning. We collect tuples of actions and observations from demonstrations, and used supervised learning to learn a policy \(\pi_{\theta}(a_t | o_t)\).

The problem with behavioural cloning is that the errors accumulate, and the state trajectory will change dramatically. When we evaluate the algorithm, can we make \(p_{data}(o_t) = p_{\pi_\theta}(o_t)\)?

DAgger: Dataset Aggregation

  • Goal: collect training data from \(p_{\theta_\pi}(o_t)\) instead of \(p_{data}(o_t)\)
  • how? run \(\pi_\theta (a_t | o_t)\), but need labels \(a_t\)!
  1. train \(\pi_\theta(a_t | o_t)\) from human data \(\mathcal{D}\)
  2. run \(\pi_\theta(a_t|o_t)\) to get dataset \(\mathcal{D_\pi}\)
  3. Ask human to label \(D_\pi\) with actions \(a_t\)
  4. Aggregate: \(\mathcal{D} \leftarrow \mathcal{D} \cup \mathcal{D}_\pi\)
  • Problem: have to ask humans to label large datasets iteratively, and can be unnatural (resulting in bad labels)
  • Behavioural cloning may still work when we model the expert very accurately (no distributional “drift”)

Why might we fail to fit the expert?

  1. non-Markovian behaviour

    1. Our policy assumes that the action depends only on the current observation.
    2. Perhaps a better model is to account for all observations.
    3. Problem: history exacerbates causal confusion (Haan, Jayaraman, and Levine, n.d.)

  2. Multimodal behaviour

    1. Solutions:
      1. output mixture of Gaussians (easy to implement, works well in practice)
      2. Latent Variable models (additional latent variable as part of input)
      3. Autoregressive discretization
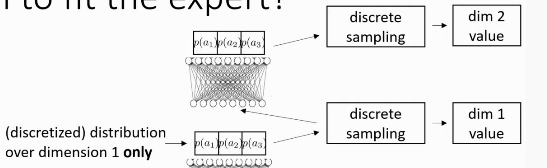
Figure 1: Autoregressive Discretization discretizes one dimension of the action space at a time

Figure 1: Autoregressive Discretization discretizes one dimension of the action space at a time

What’s the problem with imitation learning?

  • Humans need to provide data, which is typically finite. Deep models typically require large amounts of data.
  • Human are not good at providing some kinds of actions
  • Humans can learn autonomously (from experience)

Imitation Learning in the RL context

Reward function:

\begin{equation} r(\mathbf{s}, \mathbf{a})=\log p\left(\mathbf{a}=\pi^{\star}(\mathbf{s}) | \mathbf{s}\right) \end{equation}

Cost function:

\begin{equation} c(\mathbf{s}, \mathbf{a})=\left\{\begin{array}{l}{0 \text { if } \mathbf{a}=\pi^{\star}(\mathbf{s})} \ {1 \text { otherwise }}\end{array}\right. \end{equation}

The number of mistakes go up quadratically in the worst case:

Assuming: \(\pi_{\theta}\left(\mathbf{a} \neq \pi^{\star}(\mathbf{s}) | \mathbf{s}\right) \leq \epsilon\)

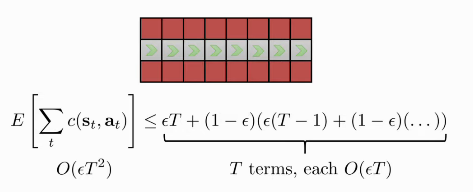
Figure 2: The tightrope walking problem

Figure 2: The tightrope walking problem

Bibliography

Haan, Pim de, Dinesh Jayaraman, and Sergey Levine. n.d. “Causal Confusion in Imitation Learning.” http://arxiv.org/abs/1905.11979v2.

Links to this note