Deep Reinforcement Learning
Why Deep Reinforcement Learning?
- Reinforcement learning provides a mathematical framework for decision-making
- Deep learning has shown to be extremely successful in unstructured environments (e.g. image, text)
- Deep RL allows for end-to-end training of policies
- Features are tedious and difficult to hand-design, and are not so transferable across tasks
- Features are informed by the task
Anatomy of Deep RL algorithms
\begin{equation} \theta^{\star}=\arg \max _{\theta} E_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t} r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right] \end{equation}
- policy gradients
- directly differentiate above objective
- value-based
- estimate value/q-function of the optimal policy (no explicit policy)
- actor-critic
- estimate value/q-function of the current policy, use it to improve policy
- model-based RL
- estimate the transition model, and then…
- use it for planning (no explicit policy)
- Trajectory optimization/optimal control (continuous spaces)
- Discrete planning in discrete action spaces (Monte Carlo Tree Search)
- use it to improve a policy (e.g. via backpropagation, with some tricks)
- use the model to learn a value function (e.g. through dynamic programming)
- use it for planning (no explicit policy)
Why so many RL algorithms?
- Different tradeoffs
- sample efficiency
- is it off policy: can improve policy without generating new samples from that policy?
- however, are samples cheap to obtain?
- sample efficiency
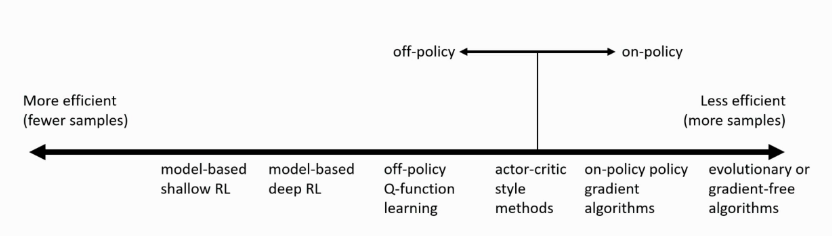
Figure 1: Sample efficiency comparison
- stability and ease of use (does it converge, and if so to what?)
- Q-learning: fixed point iteration
- Model-based RL: model is not optimized for expected reward
- Different assumptions
- fully observable?
- generally assumed by value function fitting methods (mitigated by adding recurrence)
- episodic learning
- generally assumed by pure policy gradient methods
- assumed by some model-based RL methods
- continuity or smoothness?
- assumed by some continuous value function learning methods
- often assumed by some model-based RL methods
- stochastic or deterministic?
- fully observable?
- Different things are easy or hard in different settings
- easier to represent the policy?
- easier to represent the model?
Challenges in Deep RL
Stability and Hyperparameter Tuning
- Devising stable RL algorithms is hard
- Can’t run hyperparameter sweeps in the real world
Would like algorithms with favourable improvement and convergence properties:
- Trust region policy optimization Schulman et al., n.d.n
or algorithms that adaptively adjust parameters:
- Q-Prop Gu et al., n.d.
Problem Formulation
- Multi-task reinforcement learning and generalization
- Unsupervised or self-supervised learning
Resources
- CS285 Fall 2019 - YouTube
- Welcome to Spinning Up in Deep RL! — Spinning Up documentation (Tensorflow, Pytorch)
- David Silver’s Deep RL ICML Tutorial
<biblio.bib>