Model-Based Reinforcement Learning

In model-free Reinforcement Learning ⭐, we assumed that \(p(s_{t+1} | s_t, a_t)\) is unknown, and no attempt is made to learn it. However, we often know the dynamics. For example, in games such as chess, and easily modeled systems, like car navigation.

Model-based Reinforcement learning is about learning system dynamics, and using the learnt system to make decisions.

In the stochastic open-loop case,

\begin{equation} p_{\theta}(s_1, \dots, s_T | a_1, \dots, a_T) = p(s_1) \prod_{t=1}^{T} p(s_{t+1} | s_t, a_t) \end{equation}

and we’d want to choose:

\begin{equation} a_1, \dots, a_T = \mathrm{argmax}_{a_1, \dots, a_T} E \left[ \sum_{t} r(s_t, a_t) | a_1, \dots, a_T \right] \end{equation}

In a closed-loop setting, the process by which the agent performs actions receives feedback. Planning in the open-loop case can go extremely awry.

In the stochastic closed-loop case,

\begin{equation} p(s_1, a_1, \dots, s_T, a_T) = p(s_1) \prod_{t=1}^{T} \pi(a_t | s_t) p(s_{t+1} | s_t, a_t) \end{equation}

where \(\pi = \mathrm{argmax}_{\pi}E_{\tau \sim p(\tau)} \left[ \sum_t r(s_t, a_t)\right]\)

Simple Model-based RL

The most basic algorithm does this:

1. Run base policy to obtain tuples \((s_{t+1}, s_t, a_t)\)
2. Use supervised learning on the tuples to learn the dynamics \(f(s_t, a_t)\), minimizing loss \(\sum_i |f(s_t, a_t) - s_{t+1}|^2\)
3. Use the learnt model for control

Problem: distributional shift. We learn from some base distribution \(\pi_{0}\), but control via \(\pi_{f}\). This can be addressed by re-sampling \((s, a, s’)\) to \(D\) after step 3.

Performance gap in model-based RL

Model-based RL tends to plateau in performance much earlier than model-free RL. This is because it needs to use a function approximator that:

1. Does not overfit a low amount of samples
2. But also is expressive enough

And this turns out to be hard. Below, the model is overfitted, and the planner might want to exploit going to this non-existent peak, and result in nonsensical behaviour.

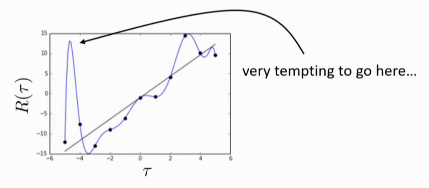We can use uncertainty estimation to detect where the models may be wrong, for example by using Gaussian Processes.

For planning under uncertainty, one can use the expected value, optimistic value, or pessimistic value, depending on application.

How can we have uncertainty-aware models?

1. Use output entropy: high entropy means model is uncertain.
   1. But model might overfit and be confident, but wrong!
2. Estimate model uncertainty: the model is certain about the data, but we are not certain about the model.
   1. estimate \(\log p(\theta | D)\)
3. Or use Bayesian NN, Bootstrap ensembles

Problems with model-based RL

1. High dimensionality
2. Redundancy

Partial observability

Latent space models: separately learn \(p(o_t | s_t)\) (observation model; high dimensional, but not dynamic) and \(p(s_{t+1} | s_t, a_t)\) (dynamics model; low dimensional, but dynamic), and \(p(r_t | s_t, a_t)\) (reward model).