Data Structures and Algorithms

Java

Access Modifier

C: Class; P: Package; SC: Subclass; W: World

Comparable

Implement Comparable<T>:

int compareTo(T o)

hashCode

• If two objects are equal, hashCode must return the same result
• hashCode must return the same result hen invoked on the same object more than once

  int hashCode() {}
  boolean equals(Object o) {}

Common Issues

Array out of bounds; divide by zero; infinite loop; exception thrown but not caught; access member variable in static method

Algorithmic Analysis

Amortized Cost

Algo has amortized cost \(T(n)\) if ∀ k ∈ \mathbb{Z}, cost of k operations is \(\leq kT(n)\)

Master’s Theorem

\(T(n) = aT(\frac{n}{b}) + f(n)\) where a ≥ 1, b > 1

• \(f(n) \in O(n^c)\text{, } c < \log_ba \ \text{ then } T(n) \in \Theta(n^{\log_ba})\)
• \(f(n) \in O(n^c\log^kn)\text{, } c = \log_ba \ \text{ then } T(n) \in \Theta(n^c\log^{k+1}n)\)
• \(f(n) \in O(n^c), c > \log_ba \text{ and } \exists k \ \text{ st } af(\frac{n}{b})\le kf(n) \text{ then } T(n) \in \Theta(n^{\log_ba})\)

Common Ones

• \(T(n) = T(n/2) + \Theta(1) = O(\log n)\) (Binary Search)
• \(T(n) = 2T(n/2) + \Theta(1) = O(n)\) (Binary Tree Traversal)
• \(T(n) = 2T(n/2) + \Theta(\log n) = O(n)\) (Optimal Sorted Matrix Search)
• \(T(n) = 2T(n/2) + O(n) = O(n \log n)\) (Merge Sort)

Abstract Data Types

Bag

Insert(i); Draw()

Stack (LIFO)

empty(); peek(); pop(); push(i)

Queue (FIFO)

add(); offer(i); peek(); poll(); remove()

Dequeue

double-ended queue

Searching

• Binary Search \(O(\log n)\)

  int binarySearch(int[] arr, int key) {
      int start = 0, end = arr.length - 1;
      int found = -1;
      while(start <= end) {
          int mid = start + (end - start)/2;
          if(arr[mid] < key) {
              start = mid + 1;
          } else if(arr[mid] > key) {
              end = mid - 1;
          } else {
              found = mid;
              // if we want first instance
              end = mid - 1;
              // if we want last instance
              // start = mid + 1;
          }
      }
      return found;
  }

One sided Binary Search

Suppose one side is bounded, eg [1, ∞). Use the sequence [1,2,4,8,16…, \(2^k\)…] If it works for \(2^k\), then search on [\(2^{k-1}, 2^k\)]

Peak Finding

A[j] in array A is peak if (i) A[j] > A[j-1] (ii) A[j] > A[j+1]. If only one item in array, vacously true

1D Peak Finding \(O(\log n)\)

D&C

  if a[n/2] < a[n/2-1] look at 1..n/2-1
  else if a[n/2] < a[n/2+1] look at n/2+1..n
  else return a[n/2]

2D Peak Finding \(O(m + n)\)

D&C

  find max in border + cross O(m+n)
  if max is peak return
  else go into quadrant with higher number

Sorting

Bubble Sort

Stable, In-place, W&A \(O(n^2)\), B \(O(n)\), S \(O(1)\); Invariant : At iteration i , the sub-array A[1 .. i] is sorted and any element in A[i + 1 .. A . size] is greater or equal to any element in A[1 .. i]

Selection Sort

In-Place, Unstable; find minimum element and swap. W,A,B \(O(n^2)\), S \(O(n/1)\); Invariant: a[0…i-1] is sorted all entries in a[i..n-1] are larger than or equal to the entries in a[0..i-1]

Insertion Sort

In-place, Stable; W \(O(n^2)\), B \(O(n \log n)\), S \(O(n)\); Invariant: The subarray a[i] consists of the original elements in sorted order.

Merge Sort

Stable, In Place; W/B \(O(n\log n)\), S \(O(n)\)

Quick Sort

In-place, Unstable; W \(O(n^2)\), A/B \(O(n\log n)\) S \(O(\log n)\)

Geometric Algorithms

Jarvis March \(O(hn)\)

1. Find somewhere to start, e.g. y-min coordinate
2. Add point with maximum angle from horizon \(O(n)\)
3. Keep adding points with maximum angle from previous

Line Intersection Algorithm \(O(n\log n)\)

1. Divide into two equal size sets (along vertical line)
2. Recursively find convex hulls (base case 3 points)
3. Merge convex hulls
   1. Find upper tangent lines
      1. while \((u,v,w)\) clockwise, decrement \(v\)
      2. while \((v,w,z)\) clockwise, increment \(w\)
   2. Find lower tangent lines
      1. while \((w,v,u)\) clockwise, increment \(v\)
      2. while \((z,v,u)\) clockwise, decrement \(w\)

Quick Hull \(O(n \log n)\)

1. Choose pivot, construct two subproblems, delete interior points
2. recurse on subproblems

Trees

Binary Trees (height h)

\(h(v) = max\left(h(v.left), h(v.right)\right) + 1\)

• BST: left ST < key < right ST
• traversal \(O(n)\) IN:LSR, PRE:SLR, POST:LRS
• insert, search, findMax, findMin: \(O(h)\)
• successor \(O(h)\):
  • if hasRightChild, smallest node in right sub-tree
  • else, first parent node that is left child (parent of node is successor)
• delete \(O(h)\): switch numChild
  • 0: remove v
  • 1: remove v, connect child(v) to parent(v)
  • 2: swap with successor(v), remove(v)

AVL Trees (height \(h = \log n\))

• Property: Every node is height-balanced
• \(\lvert v.left.height - v.right.height \rvert \le 1\)

• insert \(O(\log n)\):
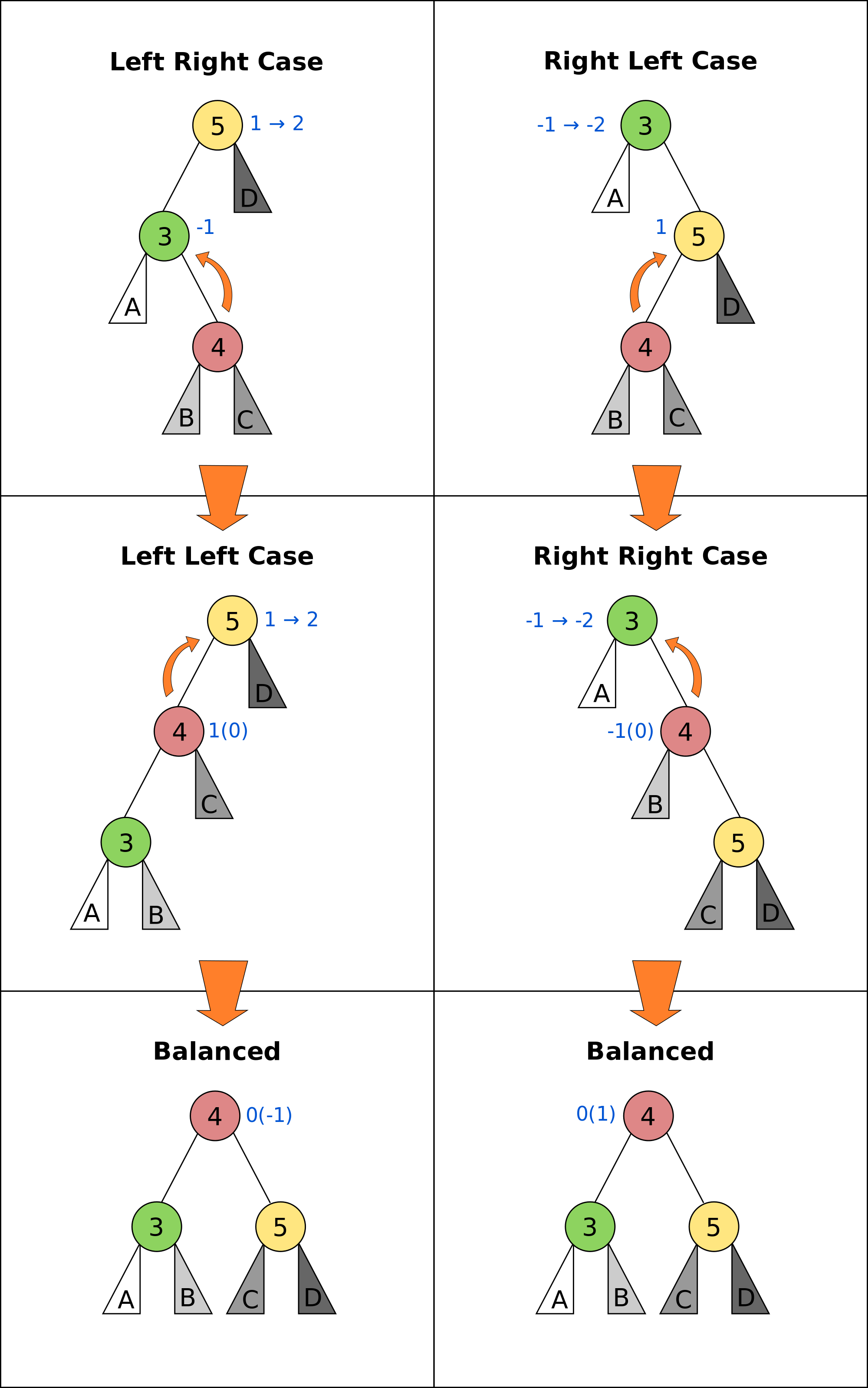
  • insert key in BST
  • walk up, perform max 2 rotations if out-of-balance
• delete(v): (\(\log n\) rotations)
  • If v has 2 children, swap with successor
  • delete v, and reconnect children
  • for every ancestor of deleted node
    • rotate if out-of-balance
• Splay Trees: Rotate nodes that are accessed to root. consider using where operations are non-random.

Augmented Trees

Rank Tree (Order Statistics)

• store weight of tree in each node:
• \(w(v) = w(v.left) + w(v.right) + 1\)
• select(k) \(O(\log n)\): finds node with rank \(k\)

  rank = left.weight + 1;
    if (k == rank)
      return v
    else if (k < rank)
      return left.select(k)
    else return right.select(k-rank)

• rank(v) \(O(\log n)\): computes rank of node v

  rank = v.left.weight + 1
    while (v != null) do
      if v is left child do nothing
      if v is right child,
         rank += v.parent.left.weight + 1
      v = v.parent

Interval Trees

• Each node is an interval \((m, n), m \le n\)
• Sort by \(m\), augment node with maximum \(n\) of children in each node
• search(x) \(O(\log n)\):

  if x in c
    return c
  else if c has no left child
    search in right subtree
  else if x > max endpoint in c.left
    search in right subtree
  else search in left subtree

• findAll(x) \(O(k \log n)\) for k overlapping intervals

  search(x)
  store it somewhere else
  remove interval
  repeat until no intervals found

Orthogonal Range Searching

• 1D

  1. use a binary tree search tree
  2. store all points in the leaves of the tree, internal nodes store only copies
  3. each internal node v stores the max of any leaf in the left subtree
  4. Query Time: \(O(k + \log n)\)
  5. Building Tree: \(O(n \log n)\)

• k-dim Tree

  1. each node in the x-tree has a set of points in its subtree
  2. store the y-tree at each x-node containing all points
  3. Query Time: \(O(k + \log^d n)\)
  4. Building Tree: \(O(n \log^{d-1}n)\)
  5. Space: \(O(n \log^{d-1}n)\)

Custom Augmentations

• Average height of people taller: augment nodes to include the count of the number of nodes in that sub-tree, along with the sum of the heights of all the people in that sub-tree. To return the desired average, first search for the name in the hash table; assume it is at node v; then find the sum of the heights of: the right-child of v, and if w is on the path from v to the root and v is in w’s left-subtree, then w’s right-subtree and w.

Hash Tables

• n: #items, m: #buckets
• Simple Uniform Hashing: Keys are equally likely to map to every bucket, and are mapped independently
  • \(load(ht) = \frac{n}{m}\)
  • \(E_\text{search} = 1 + \frac{n}{m}\)
  • Assume \(m=\Omega(n)\), \(E_\text{search} = O(1)\)

Hash Functions

Division

• \(h(k) = k \text{ mod } m\), choose m prime

Multiplication

• fix table size: \(m=2^r\), for some \(r\)
• fix word size: \(w\), size of key in bits
• fix odd constant \(A\), \(A > 2^{w-1}\)
• \(h(k) = (Ak) \text{ mod } 2^w » (w - r)\)

Rolling Hash

• When key changes by single character

Chaining

• bucket stores linked list, containing (object, value)
• Worst insert \(O(1 + cost(h))\)
• Expected search = \(1 + \frac{n}{m} = O(1)\)
• Worst search \(O(n)\)

Open Addressing

• One item per slot, probe sequence of buckets until find only one
• \(h(key, i) : U \mapsto {1..m}\), \(i\) is no. of collisions
• search: keep probing until empty bucket, or exhausted entire table
• delete: set key to tombstone value, so probe sequence still works
• insert: on deleted cell, overwrite, else find next available slot
• good hash function:
  1. \(h(key, i)\) enumerates all possible buckets
  2. Simple Uniform Hashing
• Linear: \(h(k,i) = h(k) + i\), Clustering
• Double: \(h(k,i) = f(k) + i \cdot g(k) \text{ mod } m\)
• Insert, Search: \(\frac{1}{1-\alpha}\) where \(\alpha = \frac{n}{m} \le 1\)
• good: saves space, rare mem alloc, better cache perf
• bad: sensitive to hash, load

Cuckoo Hashing

• Resolving hash collisions with worst-case constant lookup time
• Lookup: inspection of just two locations in the hash table
• Insertion: Insert into first table if empty; else kick out other key to second location.
• If infinite loop, hash function is rebuilt in place

Table resizing

• Scan old table \(O(m_1)\), create new table \(O(m_2)\), insert each element \(O(1)\), total \(O(m_1 + m_2 + n)\)
• \(O(n)\) amor: if \(n == m\), \(m = 2m\), if \(n < \frac{m}{4}\), \(m = \frac{m}{2}\)

Fingerprint Hash Table (FHT)

• Vector of 0/1 bits
• no false negatives, but has false positives. \(P_{\text{no FP}} = \left(\frac{1}{e}\right)^{n/m}\)

Bloom Filter

• use \(n\) hash functions. More space per item, but require \(n\) collisions for false positive.
• \(P_{\text{coll}} = \left(1- e^{-kn/m}\right)^k\)
• Two hash functions, \(h(k)\) and \(t(k)\), two tables \(T_1\) and \(T_2\)
• insert: \(T_1[h(k)] = 1\), \(T_2[h(k)] = 1\)
• search: if \(T_1[h(k)]\) and \(T_2[h(k)]\) both 1 return true

Graphs

Simple search

• BFS/DFS do not explore all paths

BFS \(O(V+E)\)

  bfs(root)
    Q.enqueue(root)

    while Q is not empty:
      current = Q.dequeue()
      visit(current)
      for each node n adj to current
        if n not visited
          n.parent = current
          Q.enqueue(n)

DFS \(O(V+E)\)

• Same as BFS, but use stack instead of queue

Topological Sort (DAG)

• Post-order DFS
• Kahn’s Algorithm (first append all nodes with no incoming edges to result set, remove edges connected to these nodes and repeat, also O(V+E))

SSSP

Bellman-Ford \(O(EV)\)

• \(O(V^3)\) if using Adj Matrix

  do V number of times
    for (Edge e : graph)
      relax(e)

• can terminate early if no improvement
• can detect negative cycle: perform V times, then perform once more, if have changes it has negative cycle
• if all weights are the same, use BFS

Dijkstra \(O(E\log V)\)

Interesting article on how Dijkstra’s algorithm is everywhere

• Doesn’t work with negative edge weights
• can terminate once end is found

  add start to PQ
  dist[i] = INF for all i
  dist[start] = 0
  while PQ not empty
    w = pq.dequeue()
    for each edge e connected to w
      if edge is improvement
        update pq[w] O(logn)
        update dist[w]

DAG

• Toposort, relax in order
• SSSP on DAG: run topo sort, and relax edges in that order in \(O(V+E)\)
• Single Source Longest Path problem is easy on DAG: multiply edge weights by -1 and run SSSP

Heap

• implements priority queue, is a complete binary tree
• priority of parent > priority of child
• insert: create new leaf, bubbleUp
• decreaseKey: update priority, bubbleDown
• delete: swap with leaf, delete, and then bubble
• store in array:
  • \(left(x) = 2x + 1\)
  • \(right(x) = 2x + 2\)
  • \(parent(x) = \lfloor(x-1)/2\rfloor\)

Heap Sort

1. Heapify (insert n items) O(n log n)

2. Extract from heap n times (O(n log n))

3. Improvement: recursively join 2 heaps and bubble root down (base case single node) O(n)

4. O(n log n) worst case, deterministic, in-place

UFDS (weighted)

• union(p,q) \(O(\log n)\)

  • find parent of p and q
  • make root of smaller tree root of larger tree

• find(k) \(O(\log n)\)

  • search up the tree, return the root
  • (PC): update all traversed nodes parent to root

• WU with PC, union and find \(O(\alpha(m,n))\)

MST

• acyclic subset of edges that connects all nodes, and has minimum weight

Properties

1. Cutting edge in MST results in 2 MSTs
2. Cycle Poperty: \(\forall\) cycle, max weight edge is not in MST
3. Cut Property: \(\forall\) partitions, min weight edge across cut is in MST

Prim’s \(O(E \log V)\)

• Uses cycle property

  T = {start}
  enqueue start's edges in PQ
  while PQ not empty
    e = PQ.dequeue()
    if (vertex v linked with e not in T)
      T = T U {v, e}
    else
      ignore edge
  MST = T

Kruskal’s \(O(E\log V)\)

• Uses UFDS
• It is possible that some edge in the first \(V-1\) edges will form a cycle with pre-existing MST solution

  Sort E edges by increasing weight
  T = {}
  for (i = 0; i < edgeList.length; i++)
    if adding e = edgelist[i] does
    not form a cycle
      add e to T
      else ignore e
  MST = T

Boruvka’s \(O(E\log V)\)

  T = { one-vertex trees }
  While T has more than one component:
   For each component C of T:
     Begin with an empty set of edges S
     For each vertex v in C:
       Find the cheapest edge from v
       to a vertex outside of C, and
       add it to S
     Add the cheapest edge in S to T
   Combine trees connected by edges
  MST = T

Variants

1. Same weight: BFS/DFS \(O(E)\)
2. Edges have weight \(1..k\):
   • Kruskal’s
     • Bucket sort Edges \(O(E)\)
     • Union/check \(O(\alpha (V))\)
     • Total cost: \(O(\alpha(V)E)\)
   • Prim’s
     • Use array of size k as PQ, each slot holds linked list of nodes
   • insert/remove nodes \(O(V)\)
   • decreaseKey \(O(E)\)
3. Directed MST
   • \(\forall\) node except root, add minimum incoming edge \(O(E)\)
4. MaxST
   • negate all weights, run MST algo

MST Problems

• How do I add an edge (A,B) of weight k into graph G and find MST quickly?

  • Use cycle property; max edge in any cycle is not in MST
  • only add (A,B) if k is not the max weight edge
  • O(V + E) time to find max edge along A → B with DFS

• Given an undirected graph with \(K\) power plants, find the minimum cost to connect all other sites.

  • run Prim’s, use super source
  • weight of new edges are zero
  • this is a single MST

• How do I make Kruskal run faster when sorting?

  • Store edges in separate linked lists
  • To process edges in increasing weight, process all edges in one linked list then the next
  • Time: \(O(E)\) or \(O(E\alpha(m, n))\)
  • Space: \(O(E)\), need to store all \(E\) edges

• Minimum Bottleneck Spanning Tree (MBST)

  • General idea: If I use some edge e that is not in the MST to replace some edge e’ in the MST, then my max. edge is max (max edge on original MST, e).
  • Intuitively, my MST would then fulfill the condition of MBST.
  • Note: Every MST is an MBST, but not every MBST is an MST

• Find maximum distance between 2 vertices in MST

  • Bruteforce: perform DFS starting from every single location since there is only one path from any node to another
  • DFS: \(O(V+E)\), doing it \(V\) times, \(O(V(V+E)) =O(V^2)\) since \(E = V - 1\)
  • Space: \(O(V)\), need to store all the edges in MST

Floyd-Warshall (APSP)

• Shortest paths have optimal substructure
• Shortest paths have overlapping subproblems
• Idea: gradually allow usage of intermediate vertices
• Invariant: At step k, shortest path via nodes 0 to k are correct

  // precondition: A[i][j] contains weight
  //  of edge (i,j) or inf if no edge
  int[][] APSP(A) {
    // len = # vertices
    // clone A into S
    for(int k = 0; k < len; k++)
        for(int i = 0; i < len; i++)
            for(int j = 0; j < len; j++)
                S[i][j] =
                    Math.min(S[i][j],
                             S[i][k] + S[k][j]);
    return S;
  }

Network Flow

k-edge connected

Source and target are k-edge connected if there are k edge disjoint paths(don’t share edges) from source to target.

Max flow

st-cut property with minimum capacity(outgoing from s, ignore incoming to s)

Min cut

Let \(S\) be the nodes reachable from the source in the residual graph. \(T\) = all other nodes, S → T is minimum cut

Augmenting Path

path in residual graph from s to t that has no 0 weight edges

Ford-Fulkerson

1. Start with 0 flow
2. While there exists augmenting path:
   • find an augmenting path
   • compute bottleneck (min edge)
   • increase flow on the path by bottleneck capacity

Time Complexity:

• DFS: \(O(|F|E)\)
• BFS(Edmonds-Karp, shortest augmenting path): \(O(VE^2)\)
• Dinitz: \(O(V^2E)\)

Graph Algorithms on Trees

Check if connected graph is tree

Run DFS, stop when after traversing \(V-1\) edges, return true if all nodes connected and no other used edge. False otherwise. \(O(V)\)

Min Vertex Cover

• Idea: transform tree into DAG, run DP
• only two possiblities for each vertex; taken or not

  int MVC(int v, int flag) {
      int ans = 0;
      if (memo[v][flag] != -1)
          return memo[v][flag];
      else if (leaf[v]) //if v is leaf
          ans = flag;
      else if (flag == 0) {
          ans = 0;
          for(child : adjList[v]) {
              ans+= MVC(child, 1);
          }
      }
      else if (flag == 1) {
          for (child : adjList[v]) {
              ans += min(MVC(child,1),
                         MVC(child,0));
          }
      }
  }

SSSP

• On a weighted tree, any graph traversal algorithm (eg. DFS, BFS) can obtain the shortest path to any vertice in \(O(V)\)
• Weight of shortest path between two vertices is the sum of the weights of edges on the unique path

ASSP

• Run SSSP on V vertices in total \(O(V^2)\), compared to \(O(V^3)\) FW algorithm

Diameter

• Originally, run FW in \(O(V^3)\) and do an \(O(V^2)\) all-pairs check, to total \(O(V^2)\).
• Now, only need 2 \(O(V)\) traversals: DFS/BFS from any vertex \(s\) to find the furthest vertex \(x\). Then do a DFS/BFS one more time from vertex \(x\) to find furthest vertex \(y\). Length of unique path along x to y is the diameter of the tree.

Graph Modelling Techniques

1. minimum shortest path from many source to one destination: run SSSP treating destination as source.
2. multiple sources to multiple destinations: consider super source and super sink, with edge weight 0, and run Dijkstra (if no negative edge weights), BF otherwise.
3. Attempt to convert graph into a DAG and use DP techniques. Example: attaching a variable to a vertex that is monotonically decreasing
4. Shortest path between X and Y that passes through node \(A\): Compute two shortest paths; X to A, A to Y, and join the paths.

Parallel Algorithms

Parallel Fibonacci

  parallelFib(n) {
    if(n < 2) then
    return n;
    x = spawn parallelFib(n - 1);
    y = spawn parallelFib(n - 2);
    sync;
    return x + y;
  }

• Critical Path: \(T_\infty\), Parallelism = \(T_1/T_\infty\)
• \(T_\infty(n) = max(T_\infty(n - 1), T_\infty(n - 2)) + O(1) = O(n)\)
• \(T_p> T_1/p\)
• \(T_p > T_\infty\), cannot run slower on more processors
• Goal: \(T_p = (T_1/p) + T_\infty\), \(T_1/p\) is the parallel part, \(T_\infty\) is the sequential part

Matrix Addition

Before: • Work analysis: \(T_1(n) = O(n^2)\) • critical path analysis: \(T_\infty(n) = O(n^2)\) After:

  pMatAdd(A,B,C,i,j,n)
    if(n == 1)
      C[i,j] = A[i,j] + B[i,j];
    else:
      spawn pMatAdd(A,B,C,i,j,n/2);
      spawn pMatAdd(A,B,C,i,j + n/2,n/2);
      spawn pMatAdd(A,B,C,i + n/2,j,n/2);
      spawn pMatAdd(A,B,C,i + n/2,j + n/2,n/2);
      sync;

• Work Analysis: \(T_1(n) = 4T_1(n/2) + O(1) = O(n^2)\)
• Critical Path Analysis: \(T_\infty(n) = T_\infty(n/2) + O(1) = O(\log n)\)

Parallelized Merge Sort \(O(\log^3n)\)

  pMerge(A[1..k], B[1..m], C[1..n])
    if (m > k) then pMerge(B, A, C);
    else if (n==1) then C[1] = A[1];
    else if (k==1) and (m==1) then
      if (A[1] <= B[1]) then
        C[1] = A[1]; C[2] = B[1];
      else
        C[1] = B[1]; C[2] = A[1];
    else
      // binary search for j where
      // B[j] <= A[k/2] <= B[j+1]
      spawn pMerge(A[1..k/2],
                   B[1..j],
                   C[1..k/2+j])
      spawn pMerge(A[k/2+1..l],
                   B[j+1..m],
                   C[k/2+j+1..n])
      synch;

  pMergeSort(A, n)
    if (n=1) then return;
    else
      X = spawn pMergeSort(A[1..n/2], n/2)
      Y = spawn pMergeSort(A[n/2+1, n], n/2)
      synch;
      A = spawn pMerge(X, Y);