Data Visualization

References

Program

Tools

http://antv.alipay.com

How do people use visualization?

verification
analysis
exploration/discovery
presentation/storytelling
art/aesthetics

Provenance

The steps the user take in the process of visual exploration/analysis and the resulting visualizations and findings

We use provenance for:

recall
reuse and replicate
Sharing
Meta-analysis

Capture:

datasets
visualization and insight
interaction

Visual Interaction Techniques

Selecting/Highlighting/Brushing
Using Lasso to update linked views
sidebars for interactive filtering

A well-designed interactive visualization interface should show the following

Visualize: use effective visual encodings
Filter: reduce visible data to relevant items
Select: Retrieve details about interesting items
Navigate: Pan, zoom, change view

https://github.com/juba/scatterD3 DeepTree http://www.visualcomplexity.com/vc/

Visual Design and Encoding - Westermann

The purpose of visualization is insight, not pictures. - Schneiderman

Why use Interactivity?

Handle data complexity
A single static view can show only one aspect of data

Overview first, zoom and filter, then details-on-demand

Why depend on vision?

Visual system is high-bandwidth channel to brain

Pre-attentive Processing

Sequential vs. Parallel processing (popout)
Combination of channels usually requires serial search
Difficult if no unique visual property of the target

Gestalt Principles

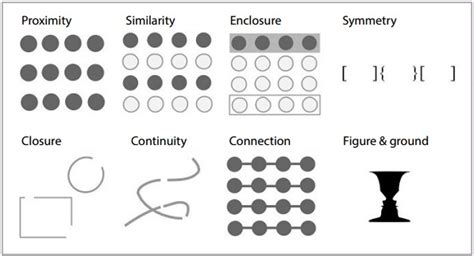
Representations should be correct, accurate and truthful.

To bring up a change, you must attend to it. (Change blindness)

Visual Design

A good visualization depends on:

data types
context of the data
tasks to perform e.g. identify trends
questions to answer
messages to deliver

\begin{equation} \text{Lie Factor} = \frac{\text{Size of effect shown in graphic}}{\text{Size of effect in data}} \end{equation}

Bad visualizations do not allow you to recover original data from the visualization. Keep proportions and relative sizes.

maximize data-ink ratio

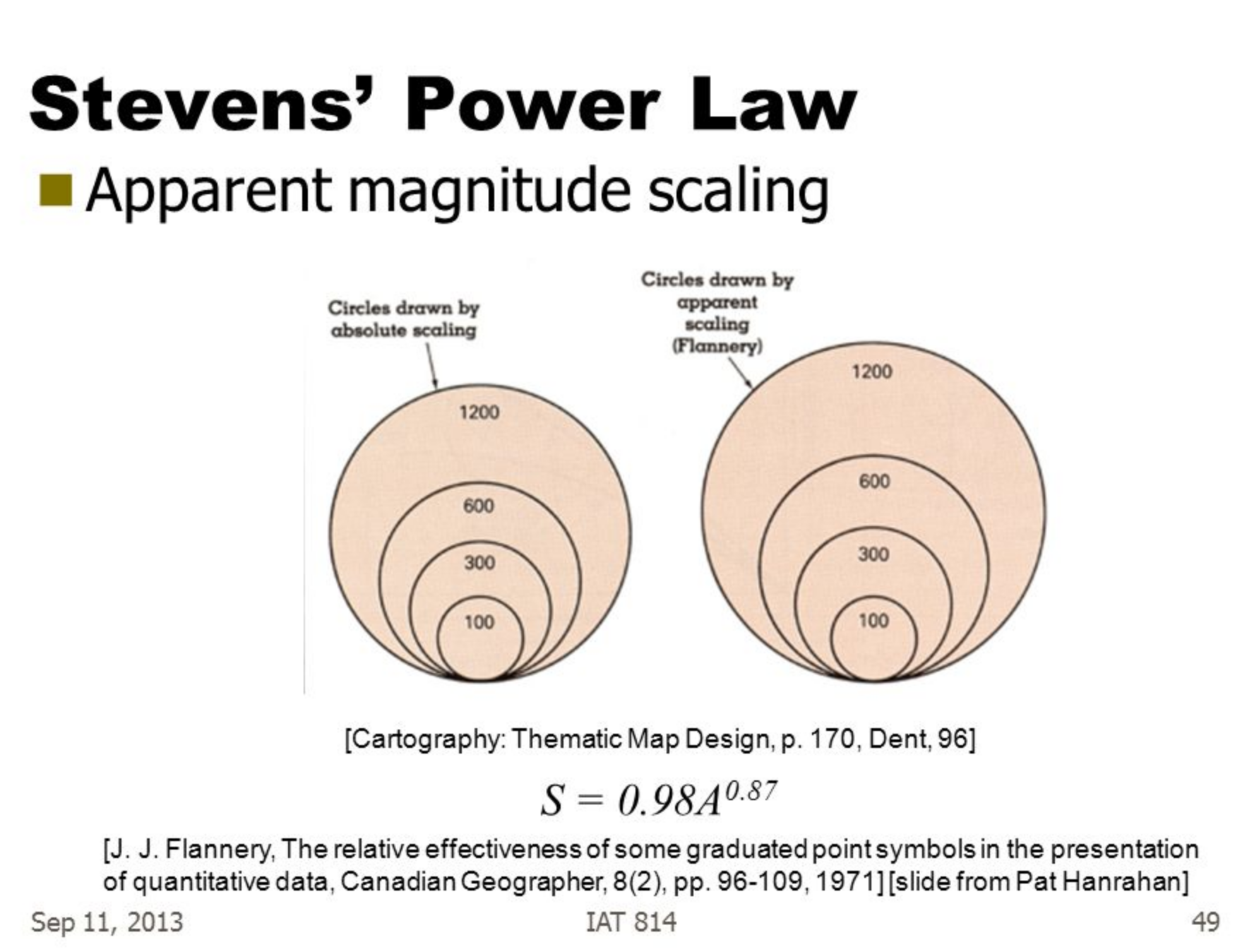
Steven’s Psychological Power Law

https://en.wikipedia.org/wiki/Stevens%27s%5Fpower%5Flaw

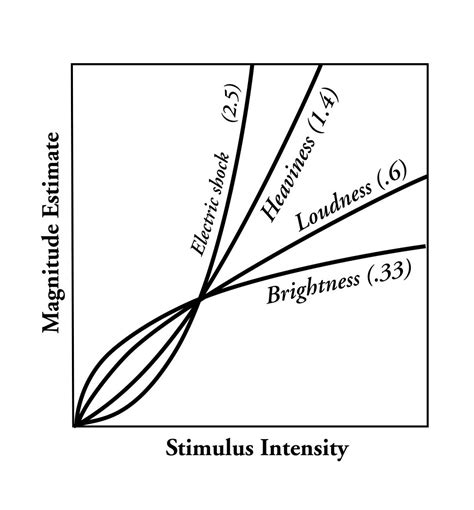Steven’s psychophysical power law:

\begin{equation} \text{Perceived sensation} = \text{Physical Intensity}^T \end{equation}

Compensating for human’s over/underestimation:

Difficult to focus on one channel when multiple channels are presented. (Redudancy is bad!)

Visual mapping - Separable vs integral visual channels

Color + position
Color + size
Width + height
Red + green* Unfiled
https://en.wikipedia.org/wiki/Tutte%5Fembedding
Reingold-Tilford Algorithm
- https://stackoverflow.com/questions/13128750/what-are-the-step-to-the-reingold-tilford-algorithm-and-how-might-i-program-it

Scientific Data Visualization - Stefan Bruckner

Types of Visualization

Volume Visualization
- Visualization of scalar fields
- Important in medicine, biology, geoscience, engineering, …
Flow Visualization
- Visualization of Vector Fields
- Data typically from computational fluid dynamics (CFD) simulations

Data Representation

Inherent Spatial Domain?
- Yes: Do we recycle data space or not
- No: Select which representation space
What dimension is used for what?
- Relationship data space <=> data attributes
- Available display space (2D/3D)
- Where is the focus?
- Where can you abstract?

Grids

Common way of storing datasets of field type (scalar, vector, tensor fields)
Typically a high-performance, space-efficient representation
Data is organized in cells which contain samples.
Often used to define an interpolation function that defines data values between samples leading to a continuous representation.
Which data orginazation is optimal?
Where does the data come from?
Is there an explicit neighbourhood relationship?
How is the neighborhood information stored?
How is navigation within the data possible?
Calculations within the data possible?
Are the data structured?

Regular Grid

Orthogonal, equidistant grid
Sample distances not equal
Implicit neighborhood-relationship

Rectilinear Grid

Orthogonal grid
Varying sample distances (\(x[i], y[j]\) given)
Allows you to place more samples in areas that are more important to you, not wasting storage in uninterested areas

Curvilinear Grid

Non-orthogonal grid
Grid-points explicitly given (\(x[i,j]\))
Implicit neighborhood relationship

Block-structured Grid

Combination of structured grids

Unstructured Grid

Grid-points and connections arbitrary
Grid-points and neighborhood explicitly given
Cells: tetrahedra

TODO Other Grids SUMMARY OF GRID TYPES

Non-cartesian Coordinates

Scattered Data

Grid-free data

Interesting to look at dimensionality of data space, vs dimensionality of data attributes

Data Enhancement

Filtering
Resampling
Data derivation
Data interpolation

Data, Visualization, Interaction

Coupling varies considerably
- Data Generation (data acquisition)
  - Mesaurement, simulation, modelling
  - Can take very long, and be very costly
- Visualization (rest of visualization pipeline)
  - Data enhancement, viz mapping, rendering
  - Depending on implementation, fast/slow
- Interaction
  - How can the user intervene, vary parameters

Interactive Steering

Simulation and modelling generate data “on the fly”
Allows real-time insight of the data
User can interfere with the simulation, and change the design of the simulations

Volume Visualization

the visualization of 3D scalar fields
Mapping 3D -> 2D
Projection (e.g. MIP), slicing, volume rendering
Volume data is 3Dx1D data
Scalar data, 3D data space, space filling
User wants to gain insight into 3D data, find structures of special interest + context

Organization of Volume Data
1. Cartesian or Regular grid
  1. CT/MR, often dx=dy<dz
  2. Data enhancement: iso-stack-calculation
2. Curvilinear, unstructured grid

Challenges

So much information, so few pixels
How to identify and enhance relevant features in the data.
Speed and interaction very important

Voxels vs Cells

pixels = picture element, voxels = volume element
A voxel is a point sample in 3D, not necessarily interpolated
Cell is a cube primitive, and the corners are 8 voxels. Values in cell use interpolation.

Linear Interpolation

Current GPUs automatically do trilinear interpolation of 3D textures

Evaluating Quality of Reconstruction

Marshner-Lobb function is a common test signal to evaluate the quality of reconstruction filters
Signal has a high amount of energy near its Nyquist frequency

Classification

Using data values, gradiant and curvature, segment data into multiple semantic regions
Often semi-automatic or fully manual
Automatic approximation: transfer functions
- Simplest example of 1D transfer function: data value -> color

Visualization Approaches

Slicing: display of 2D cross sections
Indirect Volume Rendering: Extraction of an intermediate representation
Direct Volume Rendering: Direct display of representation

TODO Isosurface Similarity

Visualization in the Spatial Domain

Slicing
- Reduce the dimensionality of 3D t o2D by showing a cross section
- Usually without a transfer function
- Orthogonal slicing often used to slice along anatomical planes in medical imagery
- Oblique slicing has arbitrary slice orientation, often used in an multi-planar reformation (MPR) setup.
- Curved slices often tailored towards specific applications, e.g. visualization of blood vessels.

Direct Volume Rendering
- Dense representation of underlying scalar field: transfer function defines visible structure.
- Image order (ray casting) fast and easy to implement, and are well supported by current GPUs
- Object order (splatting, texture slicing) also supported by older GPUs, but difficult to skip non-visible regions. Easy to skip…(?)
- Nowadays: shading/classification after interpolation/resampling
- post/pre-interpolative classification order

Ray Tracing vs Ray Casting

Ray tracing : method from image generation, usig ray-object intersection and tracing secondary rays.

Ray casting : no objects, density values in 3D, only viewing rays.

Shading

lambertian reflection : light reflected equally in all directions

specular reflection : light reflected more in one direction

Make structures in volume data sets more realistic by applying an illumination model
- Shade each sample in the volume like a surface: Blinn-Phong illumination model commonly used.
- Use normalized gradient vector as estimation for surface normal.

Indirect Volume Rendering

Extract an intermediate representation from the volume (geometric surface), then use traditional rendering methods
Cuberille regards each xovel as a little cube, classify as either part of the object or not.

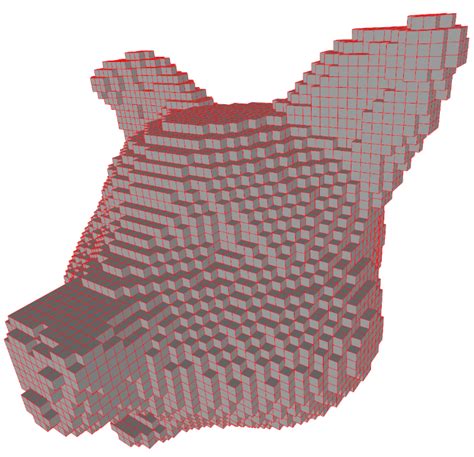
Marching Cubes is a standard method for the extraction of isosurfaces from volume data

Flow Visualization

Airplane/ship/car design
Weather simulation
Medicine (blood flows etc.)
Gaseous, liquid flow
Flow models: Differential Equation Systems (ODEs)
Common techniques for solving Navier-Stokes equations:
1. Lagrangian approach (particle-based)
  1. Treat the fluid as discrete particles, and apply interaction forces.
  2. Pros: momentum conservation/more intuitive, and fast, no linear equation solving
  3. Cons: connectivity information/surface reconstruction
2. Eulerian approach
  1. Discretize the domain using finite differences
  2. Use the operator splitting technique to solve each term separately
  3. Pros: derivative approximation, adaptive time step/solver
  4. Cons: memory usage & speed, grid artifact/resolution limitation.

Data Visualization of Text Data - Jaegul Choo

Overview

Vector encoding techniques of text
1. Bag-of-words vectors and word embedding
Basic text visualization techniques
1. Word cloud, wordle, word tree, phrase nets, ThemeRiver
Topic Modeling
1. Non-negative matrix factorization
2. UTOPIAN and visual analytic systems
Dimension reduction
1. Multidimensional scaling and tSNE
2. Interactive dimension reduction techniques and systems
Interactive visualization of deep learning
1. Toolkits: Tensorboard, Embedding Projector, Visdom
2. Advanced visual analytics systems: CNNVis, LSTMVis, DeepEyes