Cryptography
Diffie-Hellman Algorithm
https://www.youtube.com/watch?v=YEBfamv-%5Fdo&list=PL87386AD236727A1B&index=8
How can 2 people who never met agree on a secret key, without a man in a middle always listening, to figure the key out?
- One-way function
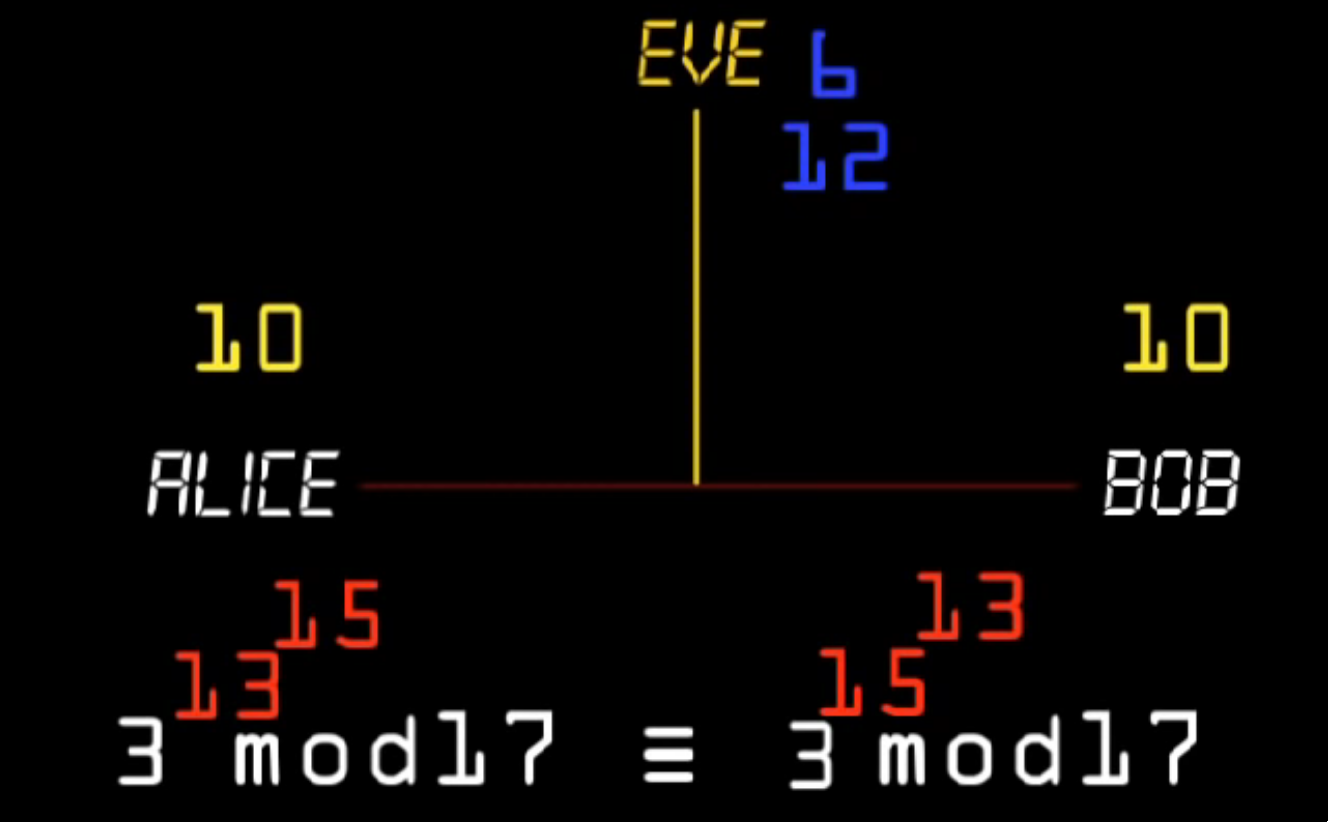
Consider a situation with 3 parties, Alice, Bob (the two parties trying to communicate) and Eve, the thief.
- Alice and Bob agree on a public colour. Eve is able to detect the public colour.
- Alice and Bob choose a private colour, and mix their private colours with the public colour and send the mixtures over. Eve is able to collect these mixtures.
- Alice and Bob add their private colour to the mixture sent by the other person, to obtain the secret colour.
Eve is unable to obtain the secret colour because it requires the private colour to obtain.
We use modular arithmetic as the numerical procedure in place of colours for the Diffie-Hellman algorithm.
We choose a prime, and a primitive root, such that \(root^x mod prime\) is uniformly distributed across all possible modulos. Modulo arithmetic is a great example on a one-way function, where computation is easy to perform in one direction, but difficult to perform in reverse.